3D Computer Graphics from Scratch
Study of 3D graphics in video games with minimal prior knowledge of mathematics
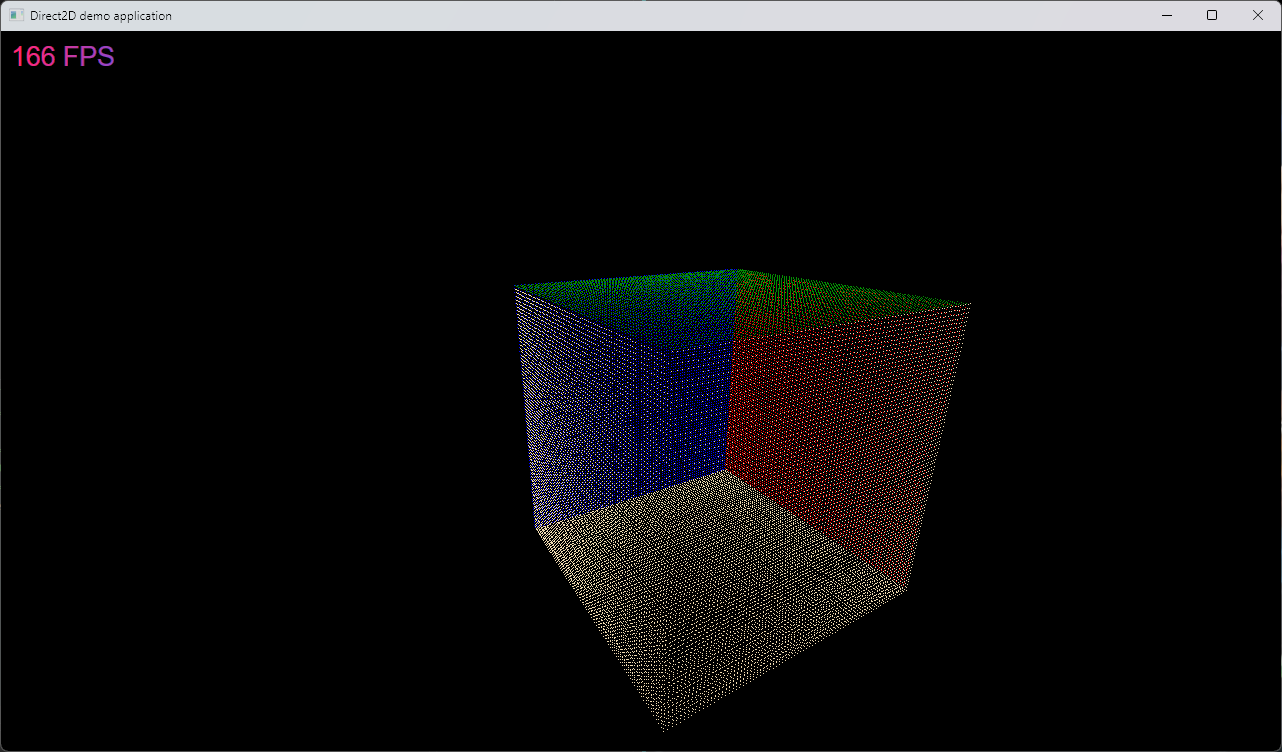
Introduction
A starting point for the introduction of 3D graphics would be to delve into its historical origins, the foundation of geometry was laid during ancient Greece with significant contributions from figures such as Thales, Pythagoras, and Euclid, who is often regarded as the "father of geometry".
- "Geometry" has its roots in Ancient Greek,
γεωμετρία(geometria) composed of two elements:
- Γῆ (Ge): This element means "Earth's land"
- Μέτρον (Metron): This element means "measure" or "measurement"
When combined, the term γεωμετρία means the study of spatial relationships defined by practical measure, analyze and describe features of the Earth's land, for real-world applications such as agriculture, construction, and navigation.
Euclid wrote a book called Element where he provided specific definitions for several fundamental geometric terms:
- «
Σημεῖόν ἐστιν, οὗ μέρος οὐθέν» could be translated by «A point is, of which part is none», this definition emphasizes the geometric indivisibility of a point, hence its only measurable attribute is the distance between two points. - «
Γραμμὴ δὲ μῆκος ἀπλατές» «A line, however, has length without breadth» emphasizing the idea that a line has only one measurable attribute, its length. - «
Γραμμῆς δὲ πέρατα σημεῖα» «The extremities of a line are points», underlying that a line is composed of points, since a line can have different length. - «
Σῶμά ἐστι τὸ μῆκος, πλάτος, βάθος ἔχον» «A solid is that which has length, breadth, and depth», meaning that a solid has 3 measurable attributes that do not overlap between them - «
Τριγώνου δεξιοῦ τὸ τετράγωνον τῆς ὑποτείνουσης τοὺς τετραγώνους τῶν περὶ τὰς ἄλλας πλευρὰς ἰσότητα πεποιήκαμεν» «In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides», we will keep this proposition to explain rotation spatial transformation later on.
With these in mind, we can build any geometric elements with just points.
Hence I do not rely on modern 3D graphics techniques to render geometric elements but the definition of points as Euclid set in his "Element" book.
Introduction
Euclid did not introduce the concepts of axes, coordinates and dimensional space as known as Cartesian coordinate system, but a comprehensive analysis of points and lines can lay down its foundation.
Euclid's statement "Γραμμῆς δὲ πέρατα σημεῖα" also highlights the spatial relationship between the endpoints of a line, the relative spatial position between them where the length tell that position.
Hence, if points do have a spatial relationship between them and if any geometric elements can be shaped with points, each points inside a geometric element possesses a unique spatial position, relative to that element.
To precisely determine the relative spatial position of a point inside a more complex geometric element other than a line, we may trace the shortest line from this point to the other point within each of the existing or imaginary measurement lines, establishing a network of interconnected points that defines their relative spatial position.
And the best candidate to build any geometric elements with a set of points is a στερεὰ (sterea), a geometrical solid such as παραλληλεπίπεδον (parallelepiped), since its lines draw the length, breadth, and depth without overlapping each others, hence each point inside a παραλληλεπίπεδον will have a set of 3 measurements/distances between them and the corresponding points within the length's line, breadth's line and depth's line of the παραλληλεπίπεδον.
Later on, those measurement components will be called coordinates, coordinates relative to the measurement lines, which will be called axes, where each axis open a dimensional space.
In ancient Greece, measurements were often based on geometric and proportional relationships rather than standardized units as we have today, hence πῆχυς (Cubit) and στάδιον (Stadion) were used as counting units to set the distance in construction.
Euclid had a Κανών (ruler) to draw his geometrical element that had no numerical value markings, a πῆχυς could not fit the size of a ruler to draw geometrical elements, hence the metric system that came in the late of 19th century was the best choice as measurement units.
Now that we have lay down the foundation of Cartesian coordinate system, we have one more study to achieve, while we logically can move a point on a straight line by adding a variable number to one of its 3 measurement components, we have one spatial transformation left, moving a point on curved line, known as rotation.
And the rotation do have the circle as perfect geometric candidate since it has a single reference point located in its center for all points inside, visually rotating around the said reference point.
As Euclid stated above «In a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides», emphasizing that a right-angled triangle had a spatial relationship between its three line's length, such as, known as Pythagorean theorem:
HypotenuseLength × HypotenuseLength = FirstSideLength × FirstSideLength + SecondSideLength × SecondSideLength
While we could use that way to rotate points, the lack of a rotation measurement known as angle, will rotate the points without accuracy
Unfortunately, I haven't found a connecting bridge between the Pythagorean theorem and trigonometric functions that is using angles instead of using a right-angled triangle properties to draw a circle, thus the comprehensive analysis of Euclid's book stop here and we must leap toward modern geometry era.
Trigonometric functions such as sin(θ) and cos(θ) where θ represent the angle of a point on the circle's line relative to the measurement X line of the circle and return the corresponding relative position to its measurement lines.
Those measurement lines are commonly called X and Y

Hence, we will start with a visual study of the trigonometric circle to achieve rotation of points.
First we set a point at 0° (x = 1, y = 0) and we apply a rotation on this point by +90° (+ is anticlockwise and - is clockwise) around the center, the result to find is x = 0, y = 1.
And the general formulas to find this result is:
X′ = X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
It's relatively simple to retrieve this equation from scratch and later, we will see that this formulas is just the linear form of the Z rotation matrix.
Here's the methodology:
- We have a circle with two measurement lines (known as 2D) with a radius of 4.
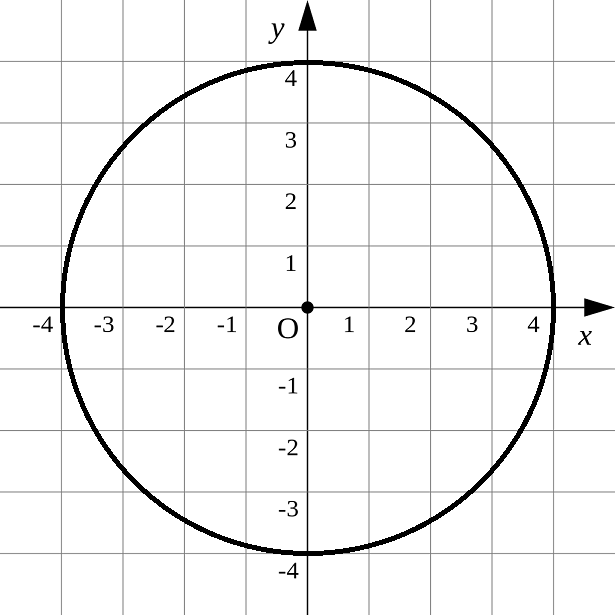
- We set a point, rotate it and try to retrieve the equation that lead to its new position, thus once we have operate on a P(X, 0) and P(0, Y) combinations, we will find the equation to rotate any P(X, Y)
- Let's begin with P(4, 0), visually a red dot:

- We rotate this point of +90° and try to find the equation of its new position, visually the result to find is P(0, 4):

X = sin(θ) = 1 ❌ X = cos(θ) = 0 ✔ Y = cos(θ) = 0 ❌ Y = sin(θ) = 1 ❌✔ Y = 4 × sin(θ) = 4 ✔
- So for P(4, 0) with θ = 90, we have:
X′ = cos(θ) Y′ = X × sin(θ)
- Trying with other angles for P(4, 0) give a slightly different equations (using mathsisfun) but where combined, gives this result:
-
X′ = 4 × cos(θ) = X × cos(θ) Y′ = 4 × sin(θ) = X × sin(θ)
- Now we set the red point at P(0, 4):

- We rotate this point of +90°, visually the result is P(-4, 0):

X = cos(θ) = 0 ❌ X = sin(θ) = 1 ❌✔ X = 4 × -sin(θ) = -4 ✔ Y = sin(θ) = 1 ❌ Y = cos(θ) = 0 ✔
- So for P(0, 4) and θ = 90, we have:
X′ = Y × -sin(θ) Y′ = cos(θ)
- Trying with other angles for P(0, 4) give a slightly different equations but where combined, gives this result:
X′ = 4 × -sin(θ) = Y × -sin(θ) Y′ = 4 × cos(θ) = Y × cos(θ)
- Now let's summarize:
_________________ _________________ | | | | P(X, 0) | P(0, Y) | |_________________|_________________| | | | | X′ = X × cos(θ) | X′ = Y × -sin(θ)| | Y′ = X × sin(θ) | Y′ = Y × cos(θ)| |_________________|_________________|
As we can see, the situation where X or Y equal 0 do generate different equations, let's see what happen when X and Y values are below 4 and above 0:
- Hence, we set the point at P(2, 4×√3/2):

- Now we rotate this point of +30°, visually the result to find is P(0, 4):

X = sin(θ) = 0.5 ❌ X = cos(θ) = √3/2 ❌ Y = sin(θ) = 0.5 ❌ Y = cos(θ) = √3/2 ❌
We have a problem, none of the trigonometric functions work, so we need to find the solution elsewhere.
Let's review the previous equations found:
_________________ _________________ | | | | P(X, 0) | P(0, Y) | |_________________|_________________| | | | | X′ = X × cos(θ) | X′ = Y × -sin(θ)| | Y′ = X × sin(θ) | Y′ = Y × cos(θ)| |_________________|_________________|
What will happen if we have X and Y above 0, it should be a mix of both of them:
X′ = X × cos(θ) X′ = Y × -sin(θ)
Y′ = X × sin(θ) Y′ = Y × cos(θ)
X′ = X × cos(θ) Y × -sin(θ)
Y′ = X × sin(θ) Y × cos(θ)
Let's see if an addition is working:
X′ = X × cos(θ) + Y × -sin(θ)
X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
X′ = 2 × cos(θ) - 4×√3/2 × sin(θ) = 0 ✔
Y′ = 2 × sin(θ) + 4×√3/2 × cos(θ) = 4 ✔
Perfect, this equation is giving correct result, so at the end, the final equations on a XY plane is:
X′ = X × cos(θ) - Y × sin(θ)
Y′ = X × sin(θ) + Y × cos(θ)
To close this visual study, let's try with P(X, 0) and P(0, Y):
- A rotation being applied on P(4, 0) of +90°, visually the result to find is P(0, 4):
X′ = 4 × cos(θ) - 0 × sin(θ) = 0 ✔ Y′ = 4 × sin(θ) + 0 × cos(θ) = 4 ✔
- A rotation being applied on P(0, 4) of +90°, visually the result to find is P(-4, 0):
X′ = 0 × cos(θ) - 4 × sin(θ) = -4 ✔ Y′ = 0 × sin(θ) + 4 × cos(θ) = 0 ✔
Now that we have retrieve the general formulas for rotating a point P(X, Y) on a XY circle from scratch, we can jump on rotation matrices study.
-
As said earlier, this formulas is just a linear form of the Z rotation matrix (XZ plane rotation matrix), multiplied by the measurement components of the point, also called vector.
Rotation matrix on z: Vector: _______________ _______________ _______________ _______________ | | | | | | | cos(θz) | -sin(θz) | 0 | | x | |_______________|_______________|_______________| |_______________| | | | | | | | sin(θz) | cos(θz) | 0 | × | y | |_______________|_______________|_______________| |_______________| | | | | | | | 0 | 0 | 1 | | z | |_______________|_______________|_______________| |_______________|
A 3D coordinate system can be described with several 2D coordinate systems, such as every planes drive the rotation spatial transformation everywhere in a 3D coordinate system.
Thus, we need to gather all those 2D rotation matrices that do compose a 3D coordinate system and there are 3 of them:
X Rotation Matrix (XY Plane Rotation Matrix)
_______________ _______________ _______________
| | | |
| 1 | 0 | 0 |
|_______________|_______________|_______________|
| | | |
| 0 | cos(θx) | -sin(θx) |
|_______________|_______________|_______________|
| | | |
| 0 | sin(θx) | cos(θx) |
|_______________|_______________|_______________|
Y Rotation Matrix (YZ Plane Rotation Matrix)
_______________ _______________ _______________
| | | |
| cos(θy) | 0 | -sin(θy) |
|_______________|_______________|_______________|
| | | |
| 0 | 1 | 0 |
|_______________|_______________|_______________|
| | | |
| sin(θy) | 0 | cos(θy) |
|_______________|_______________|_______________|
Z Rotation Matrix (XZ Plane Rotation Matrix)
_______________ _______________ _______________
| | | |
| cos(θz) | -sin(θz) | 0 |
|_______________|_______________|_______________|
| | | |
| sin(θz) | cos(θz) | 0 |
|_______________|_______________|_______________|
| | | |
| 0 | 0 | 1 |
|_______________|_______________|_______________|
Finally, in order to achieve a rotation on Euclid's points in a 3D coordinate system, we do need to multiply the 2D rotation matrices above, between them and where the order of the multiplication matters, but we will take a closer look on that in the next tutorial heading this one.
History
- 1st February, 2024: Article/Code update, starting from Euclid's works to explain computer graphics.
- 12th June, 2018: Initial version
