Exploring Computational Number Theory (Part 3)
5.00/5 (5 votes)
Factoring classic integers
C#
- Download source - 47.3 KB
- Download BigIntegerExcelDNA.zip - 2.3 MB
- Download ExcelDna-0.32.zip - 1.4 MB
VBA
Excel
Word
Introduction
In Exploring Computational Number Theory (Part 1)" a process for determining the Euler prime/pseudoprimes to any positive integer exponent was described. In "Semi-Prime Ordered Sequences (Part 2)" a process for ordering the semi-prime binary sequences over an infinite domain was described.
This article explains a method for factoring classic integers. As in "Exploring Computational Number Theory (Part 1)", the use of other authors’ source materials for support in producing this article is as follows:
- "BigInteger Library" by Mihnea Rădulescu, 23 Sep 2011 at http://www.codeproject.com/Articles/60108/BigInteger-Library
- "C# BigInteger Class" by Chew Keong TAN, 28 Sep 2002 at http://www.codeproject.com/Articles/2728/C-BigInteger-Class
- "Using C# .NET User Defined Functions (UDF) in Excel" by Adam Tibi, 13 Jun 2013 at http://www.codeproject.com/Articles/606446/UsingplusC-plus-NETplusUserplusDefinedplusFuncti
- Excel-DNA Version 0.32 can be obtained from here http://exceldna.codeplex.com/releases/view/119190 .
- "Performance Tests: Precise Run Time Measurements with System.Diagnostics.Stopwatch" by Thomas Maierhofer (Tom), 28 Feb 2010 at http://www.codeproject.com/Articles/61964/Performance-Tests-Precise-Run-Time-Measurements-wi
Background
In "Exploring Computational Number Theory (Part 3)" a process for factoring the classic integers of Mersenne, 2n – 1, Fermat Lucas 2n + 1 and Euler that were presented in "Exploring Computational Number Theory (Part 1)" will be expanded. Exhibit 1 below presents time resources utilized to generate the tables used in each step of the factoring process and also as a table of content for this article. These times were generated on a notebook computer running other applications, not on a real-time or optimized benchmark system. It is just a general reference of time and you can expect a wide variance from these times if you decide to regenerate the tables.
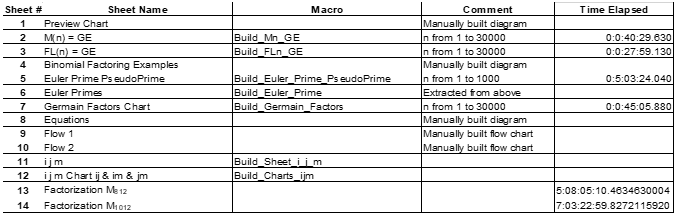
Diagram 1 below outlines the hierarchical structure of the classic integers and their relationship to each other and the factoring process to be explored.

Mersenne
By determining the factor combinations of n, the Mersenne number can be rewritten as factors of Euler numbers. Exhibit 2 is an example of rewriting Mersenne numbers into Euler numbers.

The C# code provided with this project contains a method to determine the factor combinations from the factors of n. The following C# code generates the Euler factors for Mersenne numbers from these combinations.
if ((long)combin[0, 0] > 1)
for (index = 0; index <= fac.GetUpperBound(0); index++)
{
ord = Order(fac[index, 0].ToString(), 2);
for (jndex = 0; jndex <= combin.GetUpperBound(0); jndex++)
if ((long)combin[jndex, 0] == ord)
if (Euler((long)combin[jndex, 0]) / Convert.ToInt64(fac[index, 0]) == 1)
combin[jndex, 1] = Convert.ToInt64(combin[jndex, 1]) + Convert.ToInt64(fac[index, 1]);
}
return combin;
Fermat-Lucas
Similar to the case of Mersenne numbers, Fermat-Lucas numbers can be rewritten as factors of Euler numbers by determining the factor combinations of n. Exhibit 3 below is an example.

The following C# code generates the Euler factors for Fermat-Lucas numbers from the factor combinations of n.
while (testValue % 2 == 0)
{
testValue /= 2;
twoExp++;
}
testValue = (long)Math.Pow(2, twoExp);
for (index = 0; index <= MerE.GetUpperBound(0); index++)
{
if ((long)MerE[index, 0] % testValue == 0)
{
if (Temp == null || Temp.Length == 0)
Temp = new object[1, 2];
else
{
// Redimension Temp
Hold = new object[Temp.GetLength(0), Temp.GetLength(1)];
for (jndex = 0; jndex <= Temp.GetUpperBound(0); jndex++)
for (kndex = 0; kndex <= Temp.GetUpperBound(1); kndex++)
Hold[jndex, kndex] = Temp[jndex, kndex];
Temp = new object[Hold.GetLength(0) + 1, Hold.GetLength(1)];
for (jndex = 0; jndex <= Hold.GetUpperBound(0); jndex++)
for (kndex = 0; kndex <= Hold.GetUpperBound(1); kndex++)
Temp[jndex, kndex] = Hold[jndex, kndex];
}
Temp[Temp.GetUpperBound(0), 0] = MerE[index, 0];
Temp[Temp.GetUpperBound(0), 1] = MerE[index, 1];
}
}
return Temp;
Diagram 2 & 3 below are two examples of binomial factoring of Mersenne numbers. Although this method is not needed for factoring, once the Mersenne and Fermat-Lucas numbers are rewritten as Euler numbers, it is included here for understanding and completeness.


Euler
In "Part 1" Euler numbers were derived and defined as En = 1 mod n and that En = c * n + 1 where c is a positive integer and n is the least positive exponent base 2. Exhibit 4 below indicates the Euler numbers that are prime with n <= 1000. The Miller-Rabin probability test was used to ascertain primality. Also, in Exhibit 4 are E1 = 1 and E6 = 1 which are marked as "FALSE".

Germain
In Part 1 Germain numbers were defined as Gn = c*n+1 where c is a positive integer and n is the least positive exponent base 2. If n is odd or n = 2x, then Gn = 2k*n+1 or c = 2k. If n is even, excepting n = 2x, then Gn = c * n + 1. In the above binomial factoring examples, there is a Germain factor in each example that must be considered. Graph 1 below indicates the distribution of these factors.

The C# code below generates the Germain factors for Mersenne and Fermat-Lucas numbers.
if (odd)
M_FL_E = Mersenne2Euler(number);
else
M_FL_E = FermatLucas2Euler(number);
for (index = 0; index <= fac.GetUpperBound(0); index++)
{
ord = Order(fac[index, 0].ToString(), 2);
if (ord % 2 == 0 || odd)
for (jndex = 0; jndex <= M_FL_E.GetUpperBound(0); jndex++)
if ((long)M_FL_E[jndex, 0] == ord)
{
if (Euler((long)M_FL_E[jndex, 0]) / (BigInteger)(fac[index, 0].ToString()) > 1)
if (Temp == null || Temp.Length == 0)
Temp = new object[1, 3];
else
{
// Redimension Temp
Hold = new object[Temp.GetLength(0), Temp.GetLength(1)];
for (kndex = 0; kndex <= Temp.GetUpperBound(0); kndex++)
for (lndex = 0; lndex <= Temp.GetUpperBound(1); lndex++)
Hold[kndex, lndex] = Temp[kndex, lndex];
Temp = new object[Hold.GetLength(0) + 1, Hold.GetLength(1)];
for (kndex = 0; kndex <= Hold.GetUpperBound(0); kndex++)
for (lndex = 0; lndex <= Hold.GetUpperBound(1); lndex++)
Temp[kndex, lndex] = Hold[kndex, lndex];
}
Temp[Temp.GetUpperBound(0), 0] = fac[index, 0];
Temp[Temp.GetUpperBound(0), 1] = fac[index, 1];
Temp[Temp.GetUpperBound(0), 2] = M_FL_E[jndex, 0];
}
}
return Temp;
Euler-Germain Factoring
The following equations form the bases for Euler-Germain factoring. See Factoring Algorithms for Selected RSA Numbers for an in-depth explanation and methodology for the integration of quadratic equations and the Pythagorean Theorem.





From Flow 1 and 2 above a list of quadratic equations, Exhibit 5 below, can be built.

 | |
| Graph 2 | Graph 3 |
 | |
| Graph 4 | Graph 5 |
 | |
| Graph 6 | Graph 7 |
Graph 2 above shows the linear nature of the Flow 1 search algorithm and Graph 3 above shows the non-linear nature of Flow 2. Because of the resource intensive nature of the Flow 2 algorithm, one can eliminate Flow 2 and rely on Flow 1. However, if i and j are relatively close in size (See Graph 3) there will be a performance degradation if the solution exists in the non-linear range. Faster performance can be achieved if i, j, and m are integrated into a low resource non-linear formula. In Part 1 it was stated that "finding Germain pseudoprimes from large Euler numbers is still very time consuming and unlike Euler numbers, at this time there seems to be no way to calculate Germain numbers directly". This is due to the open question of "Does there exist a formula that equates when orderin + 12 = n in the range min i to max i?" because all positive integer solutions must be within this range and of this form. If there are no integer solutions within this range then the integer under evaluation is prime or unity. The C# code snippet below searches for solutions using Flow 1 logic in a tight loop. There are further adaptations that can be employed to decrease time of calculation. For instance, if n is odd, both i and j are even; therefore, k – i must be even because even / odd = even.
long inc;
inc = 1;
if (i == 0)
i = 1;
if (BigInteger.IsBitSet(n, 0))
{
inc = 2;
if (BigInteger.IsBitSet(i, 0))
i++;
}
time = Stopwatch.StartNew();
BigInteger k = (E - 1) / n;
BigInteger h = BigInteger.IntegerSqrt(k);
while (k % (i * n + 1) != i && time.ElapsedMilliseconds < t && i <= h)
i += inc;
time.Stop();
Exhibit 6 and 7 are the factorization of M812 and M1012 in Diagram 2 and 3 using the C# code above.


Using the Code
This project is a concept prototype and as such does not have the user-friendly error checking of a more finished product. The C# code has been minimally changed since Part 1 and therefore is very close to the original version. The Excel-DNA software has been configured to support either a 32 or a 64-bit system. The BigInterger Library has been modified and expanded to support this project. The code should be ready to go for experimenting in C# projects, Excel VBA and Excel spreadsheets. To use in Excel open BigInteger-packed.xll in a spreadsheet and there will be two function libraries, "BigInteger" and "Number Theory". A reference to BigInteger-packed.xll in the VBA environment is required for some of the macros to build the spreadsheets used in this project or to be used in other VBA applications. Microsoft Excel requires references to the following libraries:
- Visual Basic For Applications
- Microsoft Excel 16.0 Object Library
- OLE Automation
- Microsoft Office 16.0 Object Library
- BigIntExcel
If you are using .NET 4.0 or later you may want to alter this project code to use Microsoft’s Numeric library. From my research, the division algorithm is the key to accuracy and speed.
Points of Interest
This code is not thread safe because of the "RegisterSize" function which changes the values of static fields. By removing this function, the process should be fairly straight forward in making this project thread safe. At present I have not explored the use of parallel processing in a multi-CPU environment. The maximum size of a BigInteger in Microsoft’s Excel 2007 or Excel 2016 is 32,767 decimal digits and will cause errors in calculations if this threshold is exceeded. See https://support.office.com/en-us/article/excel-specifications-and-limits-1672b34d-7043-467e-8e27-269d656771c3?ui=en-US&rs=en-001&ad=US#ID0EBABAAA=2016,_2013. The algorithm for finding the Order of a BigInteger is slow for finding an integers order with a large e. D:\BaseASeq\ProgramsC#\ExcelDna-0.32\Distribution\ExcelDnaPack.noexe should be changed to .exe before compiling the C# code. I have deleted all .exes in ExcelDNA so it will need to be recompiled or unzipped from the original zip file if you need them.
History
This is the second release of this software.
