Sort the Integers in Ascending Order
5.00/5 (1 vote)
How to find an F equation that will give you the only successor (minimum distance) of a given number detected in the list of numbers
Introduction
This article is a follow up of the article "Sort by a 2d Curve". This article discusses the search for a Sorting Algorithm in O(n).
Currently, such an algorithm doesn't exist because the Best Complexity Is O(n log(n)).
One Idea
I suppose I can find the successor of a given number by multiplying by a numerical quantity that I have called M.
There exists an algebraic formula that shows this definition.

For example, getting the successor of a given number can be:
2 = 1 * M3 = 2 * M4 = 3 * M5 = 4 * Mn + 1 = n * M
Then, it remains:

The idea is to look for an algebraic function such that the multiplication of the number n by this function gives the successor closest to n. If all elements are already sorted, the value of M will be the most accurate.
Whenever I add a new integer in the list at the end
- the previous elements of the list
- a floating value of
M - the previous issue
But I want to get an M function that takes into account the elements of the list. To find the successor of a number, this successor must be found in this given list. Thus, the floating value of M is the exact value after this number has been added to the list.
Objectives
We want to sort this whole list because its complexity is O (n). To obtain such complexity, we assume that there is a formula that will give us all successors.
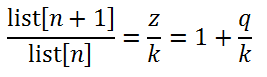
- If the list is already sorted in ascending order, then q >= 0.
- But, if the list is not completely sorted in ascending order, then q < 0.
Examples


To express a mathematical equation that takes into account all the previous values, this equation gives the same value for all the permutations of M. This means that permutations occupy an unsorted list. There is only one order, that is, a sequence of permutations that converge in the sorted list.
Sum of Values
Suppose I have n values  . If I sum all values, then any permutations of
. If I sum all values, then any permutations of  will at the same result.
will at the same result.
Now, by adding each  , we assume that it is possible to multiply this sum by a given number and this result is equal to a particular
, we assume that it is possible to multiply this sum by a given number and this result is equal to a particular  which is identified by an index position of that
which is identified by an index position of that  . Demonstration of this proposal is probably accurate, we try to take
. Demonstration of this proposal is probably accurate, we try to take  and
and  to look up their values. To do this, we want to assume that multiplying the sum by a number s will give
to look up their values. To do this, we want to assume that multiplying the sum by a number s will give  or
or  .
.




We store a list of a couple of  elements that retain the element and the previous calculated value. At each turn, we calculate the value of n. This value is the number of complete schemas.
elements that retain the element and the previous calculated value. At each turn, we calculate the value of n. This value is the number of complete schemas.
Algorithm
[<<[
print("start"),
u = [ 3, 4, 20, 5.1, 6, 7, 20, 22 ],
sum = 0,
foreach(x from u) {
sum = sum + u(x)
},
fun getIndex(sum, x) {
output(1/((sum-x)/x+1))
},
z = [],
foreach(x from u) {
z = z getIndex(sum, u(x))
},
print(z),
sum2 = 0,
foreach(x from z) {
sum2 = sum2 + z(x)
},
print(sum2),
print(z.length),
r = [],
fun toInt(x) {
n = 0,
fun selectIndice(t) {
p = [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ],
select {
break {},
default {
count = 9,
while(count >= 0) {
if (p(count) <= t) {
t = p(count),
jump "break"
},
count = count - 1
}
}
},
output(t)
},
count = 1,
while(x >= 1) {
t = selectIndice(x % 10),
x = (x-t) / 10,
n = n + t*count,
count = count * 10
},
output(n)
},
foreach(x from z) {
k = z(x) * sum / 22 * z.length * z.length,
print(k),
m = toInt(k),
print(m),
r = r m
},
print(r)
]>>]
The output is:
8,11,58,14,17,20,58,64
These numbers are radix position in an array as its size is 64 items.
History
- 24th October, 2022: Initial version
