Optimal Control of a Quadcopter
5.00/5 (27 votes)
Automatic generation of optimal control policies for the basic quadcopter flight modes
Table of Contents
- Introduction
- Quadcopter Dynamic Model
- Method
- Code
- Configuration
- Basic Flight Modes Control
- Discussion
- Conclusions
- History
Introduction
Unmanned Aerial Vehicles (UAVs) in general and multirotor helicopters, in particular, have got numerous applications. They act as technological robots, platforms for different types of equipment, like sensors, cameras, mechanical arms, weaponry, etc. They also have become a major factor on the battlefield, in law enforcement and lives saving missions (for example, this amazing "mother drone" mission saving a rare griffon vulture chick by the Israeli military). So not surprisingly, there is a flood of work devoted to the design and control of UAVs during the last years. I am also interested in this topic, as a pure hobbyist. A quadcopter was chosen as a controlled object.
Wikipedia: A quadrotor or quadcopter is a type of helicopter with four rotors.
This article presents the application of my version of Iterative Linear Quadratic Regulator (ILQR) briefly described in my CodeProject article Simple Software for Optimal Control (below referred to as [1]), to quadcopter control. The motivation was to apply a uniform approach to optimize different maneuvers of a quadcopter. The computing power of modern mobile devices mounted on quadcopters permits performing complex calculations. The calculations required for the implementation of ILQR, although quite complex, probably may be performed autonomously after appropriate code optimization. Such an approach may be used in the copter autopilot. The goal is to compute feedback on the state vector and compute independent inputs of the closed-loop system for different flight modes.

Flying quadcopter with camera (the image is taken from here).

Quadcopter (the image is taken from here).
Quadcopter Dynamic Model
From a dynamic point of view, a quadcopter constitutes a complex nonlinear system. The dynamic model of a quadcopter is described in numerous works. So, we are not going to discuss it here. Since my goal is to show the applicability of the control policy generation algorithms from [1] to quadcopter dynamics in principle, the simplified dynamic model is adopted. All effects of air resistance, turbulence due to propellers, etc. are neglected. The dynamic of electrical drives is not considered too. The math description of the model is taken mostly from here. Even with the above assumptions, the dynamic model has state vector x with a dimension of 12 and input control vector m with a dimension of 4.

Quadcopter structure and frames configuration.
Table List of Symbols
| Name | Description | Units |
| x, y, z | Position with respect to the inertial frame | m |
| xB, yB, zB | Axes of the body frame | |
| xE, yE, zE | Axes of the inertial frame | |
| φ, θ, ψ | Euler angles (roll, pitch, yaw) | rad, degrees |
| ωi | Angular velocity of rotor i | rad/s |
| M | Mass of quadcopter | kg |
| Jx, Jy, Jz | Moments of inertia | kg · m2 |
| l | Moment arm | m |
| T | Total thrust | N |
| τφ, τθ, τψ | Torques to the center of mass | m · s |
| b | Rotor drag coefficient | |
| d | Rotor thrust coefficient |
Math description of independent inputs which are open-loop control inputs - vector m:
| T = b ⋅ (ω12 + ω22 + ω32 + ω42) = m1 |
| τφ = b ⋅ l ⋅ (ω42 - ω22) = m2 |
| τθ = b ⋅ l ⋅ (ω32 - ω12) = m3 |
| τψ = d ⋅ (ω22 + ω42 - ω12 - ω32) = m4 |
As it may be seen from the above formulas, inputs mi uniquely depend on the rotors' angular velocities ωi that in their turn are controlled by the voltages of electrical motors powered rotors. These voltages for the four electrical motors are actual independent inputs to be controlled. For the sake of simplicity, here we assume a direct non-inertial dependency between motors voltages and inputs mi. This allow us to consider inputs mi, i.e., vector m as independent input of open-loop system.
Math description of the state vector x:
| x1 = | φ | ẋ1 = x2 | |
| x2 = | dφ/dt | ẋ2 = a1 ⋅ x4 ⋅ x6 + b1 ⋅ m2 | |
| x3 = | θ | ẋ3 = x4 | |
| x4 = | dθ/dt | ẋ4 = a2 ⋅ x2 ⋅ x6 + b2 ⋅ m3 | |
| x5 = | ψ | ẋ5 = x6 | |
| x6 = | dψ/dt | ẋ6 = a3 ⋅ x2 ⋅ x4 + b3 ⋅ m4 | |
| x7 = | x | ẋ7 = x8 | (1) |
| x8 = | dx/dt | ẋ8 = (cosx1 ⋅ sinx3 ⋅ cosx5 + sinx1 ⋅ sinx5) ⋅ m1 / M | |
| x9 = | y | ẋ9 = x10 | |
| x10 = | dy/dt | ẋ10 = (cosx1 ⋅ sinx3 ⋅ sinx5 - sinx1 ⋅ cosx5) ⋅ m1 / M | |
| x11 = | z | ẋ11 = x12 | |
| x12 = | dz/dt | ẋ12 = (cosx1 ⋅ cosx3) ⋅ m1 / M - g |
| a1 = (Jy - Jz) / Jx |
| a2 = (Jz - Jx) / Jy |
| a3 = (Jx - Jy) / Jz |
| b1 = l / Jx |
| b2 = l / Jy |
| b3 = l / Jz |
Table Numeric Values
| Parameter | Value | Units |
| g | 9.81 | m/s2 |
| M | 0.65 | kg |
| l | 0.23 | m |
| Jx | 7.5 · 10-3 | kg · m2 |
| Jy | 7.5 · 10-3 | kg · m2 |
| Jz | 1.3 · 10-2 | kg · m2 |
Method
The math behind this work in a very simplified manner is described in [1]. Below I will refer to pictures, denotation symbols, and formulas from [1]. Below notation [1](x) means formula x from article [1].
The quadcopter dynamic model described above is considered as an open-loop system that needs to be optimized, i.e., to minimize cost function [1](2).
 |
| Open-Loop Control System
|
The solution will be obtained as the closed-loop system:
 |
| Closed-Loop Control System
|
with parameters given in [1](7):
mk = cN-k - LN-k ⋅ xk
where:
LN-k are generally time-dependent feedback matrices from coordinates of the state vector x,
cN-k are input vectors of the closed-loop system,
N is the total number of time steps, and
k is a number of a current time step, k = 0, 1, ..., N - 1.
The dynamic system of a quadcopter is highly nonlinear (especially with considerable Euler angles). Therefore the iterative approach for the generation of L and c is used. To implement the iterative optimization, we need not only differential equations [1](1), corresponding to equations (1) above for the dynamic system, but also partial derivatives [1](9). The latter may be got either analytically or numerically ([1] provides examples for both approaches). Here, we use an analytic representation of partial derivatives called gradients in the code.
After the optimization procedure, we provide a very basic analysis of the computed feedback matrices LN-k. The average value of all components of the matrices is calculated. This "averaged" matrix may give a clue for understanding the control algorithms. Particularly, it shows the influence of the coordinates of the state vector on the inputs. In some cases, few coordinates influence just one input with their feedback. It allows us to assume that those coordinates are controlled with a separate input. In this case, the general control system with several inputs may be decomposed into several independent subsystems with a single input.
Code
The code is written in plain C# with .NET 6.0 and .NET Standard 2.0 and therefore may be run under Windows, Linux, and macOS. There is no principle difference in code compared to the software in [1]. Delegate CalcDelegate is a bit simplified with only two arguments:
public delegate double CalcDelegate(Vector m, Vector x);
Method FeedbackAnalysis() added to IBase interface and implemented in Base class, performs feedback matrices "averaging". The results are written to a text file named {caseId}_AverageFeedback.txt in the output directory. Remarkable enhancement is the Plot project to produce transients plots on the fly. It uses Python code and therefore Python3 should be installed to employ this new feature. Different optimization and simulation cases may run in parallel.
File Program.cs contains the creation and call for processing of dynamic systems. Cases Linear, VanDerPol and Rayleigh are adopted from [1] with updated code for testing purposes and commented out by default. The focal point here is Quad. Its Process() method and computing of functions and gradients are provided below:
public INonLinearQ[] Process()
{
const string Title = "Quadcopter";
Console.WriteLine($"Begin \"{Title}\"");
var outputFormat = GetOutputFormatting();
var data = DataTransformation(GetConfig<QuadData>());
(g, mass, a, b) = GetModelParameters(data);
ConcurrentBag<INonLinearQ> cbagDynamicSystem = new();
Parallel.ForEach(data.ControlCases, c =>
{
#region Iterations Settings
Vector desirableX = new(c.desirableX);
var Q = new Matrix(dimensionX, dimensionX).MakeDiag(c.diagQ);
Vector desirableU = new(c.desirableU);
var Z = new Matrix(dimensionU, dimensionU).MakeDiag(c.diagZ);
Vector xInit = new(c.xInit);
#endregion // Iterations Settings
#region Optimization
const string Act = "Optimization";
// Exact formulas for gradients computing
cbagDynamicSystem.Add(
(SQ.Create(Functions, GradientsA, GradientsB, Q, Z,
desirableX, desirableU, c.dt, xInit, c.N)
.Config(c)
.RunOptimization()
.Output2Csv(Act, outputFormat)
.Plots(DrawPlots, Act) as INonLinearQ)
.OutputExecutionDetails(isExactGradient: true)
);
#endregion // Optimization
});
// Simulation
cbagDynamicSystem.Simulate(outputFormat, data.Simulations, DrawPlots);
Console.WriteLine($"End \"{Title}\"{Environment.NewLine}{Environment.NewLine}");
return cbagDynamicSystem.ToArray();
}
private CalcDelegate[] Functions =>
new CalcDelegate[]
{
/* 1*/ (m, x) => x[_(2)],
/* 2*/ (m, x) => a[_(1)] * x[_(4)] * x[_(6)] + b[_(1)] * m[_(2)],
/* 3*/ (m, x) => x[_(4)],
/* 4*/ (m, x) => a[_(2)] * x[_(2)] * x[_(6)] + b[_(2)] * m[_(3)],
/* 5*/ (m, x) => x[_(6)],
/* 6*/ (m, x) => a[_(3)] * x[_(2)] * x[_(4)] + b[_(3)] * m[_(4)],
/* 7*/ (m, x) => x[_(8)],
/* 8*/ (m, x) => m[_(1)] / mass * ( C(x[_(1)]) *
S(x[_(3)]) *
C(x[_(5)]) + S(x[_(1)]) *
S(x[_(5)]) ),
/* 9*/ (m, x) => x[_(10)],
/*10*/ (m, x) => m[_(1)] / mass * ( C(x[_(1)]) *
S(x[_(3)]) *
S(x[_(5)]) - S(x[_(1)]) *
C(x[_(5)]) ),
/*11*/ (m, x) => x[_(12)],
/*12*/ (m, x) => m[_(1)] / mass * C(x[_(1)]) * C(x[_(3)]) - g,
};
private CalcDelegate[,] GradientsA
{
get
{
// Exact formulas for gradients computing
var gradients = InitGradients(dimensionX, dimensionX);
gradients[_(1), _(2)] = (m, x) => 1;
gradients[_(2), _(4)] = (m, x) => a[_(1)] * x[_(6)];
gradients[_(2), _(6)] = (m, x) => a[_(1)] * x[_(4)];
gradients[_(3), _(4)] = (m, x) => 1;
gradients[_(4), _(2)] = (m, x) => a[_(2)] * x[_(6)];
gradients[_(4), _(6)] = (m, x) => a[_(2)] * x[_(2)];
gradients[_(5), _(6)] = (m, x) => 1;
gradients[_(6), _(2)] = (m, x) => a[_(3)] * x[_(4)];
gradients[_(6), _(4)] = (m, x) => a[_(3)] * x[_(2)];
gradients[_(7), _(8)] = (m, x) => 1;
gradients[_(8), _(1)] = (m, x) => m[_(1)] / mass *
(-S(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + C(x[_(1)]) * S(x[_(5)]));
gradients[_(8), _(3)] = (m, x) => m[_(1)] / mass *
C(x[_(1)]) * C(x[_(3)]) * C(x[_(5)]);
gradients[_(8), _(5)] = (m, x) => m[_(1)] / mass *
(-C(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) + S(x[_(1)]) * C(x[_(5)]));
gradients[_(9), _(10)] = (m, x) => 1;
gradients[_(10), _(1)] = (m, x) => m[_(1)] / mass *
(-S(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) - C(x[_(1)]) * C(x[_(5)]));
gradients[_(10), _(3)] = (m, x) => m[_(1)] / mass *
C(x[_(1)]) * C(x[_(3)]) * S(x[_(5)]);
gradients[_(10), _(5)] = (m, x) => m[_(1)] / mass *
(C(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + S(x[_(1)]) * S(x[_(5)]));
gradients[_(11), _(12)] = (m, x) => 1;
gradients[_(12), _(1)] = (m, x) => -m[_(1)] / mass * S(x[_(1)]) * C(x[_(3)]);
gradients[_(12), _(3)] = (m, x) => -m[_(1)] / mass * C(x[_(1)]) * S(x[_(3)]);
return gradients;
}
}
private CalcDelegate[,] GradientsB
{
get
{
// Exact formulas for gradients computing
var gradients = InitGradients(dimensionX, dimensionU);
gradients[_(2), _(2)] = (m, x) => b[_(1)];
gradients[_(4), _(3)] = (m, x) => b[_(2)];
gradients[_(6), _(4)] = (m, x) => b[_(3)];
gradients[_(8), _(1)] = (m, x) => 1 / mass *
(C(x[_(1)]) * S(x[_(3)]) * C(x[_(5)]) + S(x[_(1)]) * S(x[_(5)]));
gradients[_(10), _(1)] = (m, x) => 1 / mass *
(C(x[_(1)]) * S(x[_(3)]) * S(x[_(5)]) - S(x[_(1)]) * C(x[_(5)]));
gradients[_(12), _(1)] = (m, x) => 1 / mass * C(x[_(1)]) * C(x[_(3)]);
return gradients;
}
}
After successful build Dynamics maybe run with:
dotnet Dynamics.dll
or in Windows as Dynamics.exe.
Path (either absolute or relative) to output directory is defined in App.config with parameter RootOutputDir. The output directory contains directories for optimization and simulations depending on what is computing. Each of such directories has Excel compatible CSV files with values of transients, and image files with appropriate transients plots. This output is defined in the code (method GetOutputFormatting() in Quad class and similar code for other dynamic systems). Optimization/{caseId}/Log directory also contains multiple log files for each control case with state, open-loop and closed-loop control vectors and feedback matrix for each iteration on each step. How detailed the log is, is defined by the configurable parameter logLevel.
Configuration
The software is configured with JSON configuration files. Apart from parameters of quadcopter dynamics, the files contain two arrays of parameters for ControlCases (optimization) and Simulations. In a single configuration file, Simulations array may be omitted. An example of the configuration file is provided below.
{
"g": 9.81, // m * sq(s)
"l": 0.23, // m
"m": 0.65, // kg
"Jx": 7.5e-3, // kg * sq(m)
"Jy": 7.5e-3, // kg * sq(m)
"Jz": 1.3e-2, // kg * sq(m)
// Stabilization from non-zero initial conditions
"ControlCases": [
{
"Id": "Stabilization_1-1",
"isPlotRequired": true,
"logLevel": "short",
"dt": 0.1,
"N": 61,
"maxIterations": 2,
"inDegrees": false,
"desirableX": [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],
"diagQ": [ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 ],
"desirableU": [ 0, 0, 0, 0 ],
"diagZ": [ 0, 0, 0, 0 ],
"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
},
{
"Id": "Stabilization_1-2",
"isPlotRequired": true,
"logLevel": "short",
"dt": 0.1,
"N": 61,
"maxIterations": 2,
"inDegrees": false,
"desirableX": [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 ],
"diagQ": [ 10, 1, 10, 1, 10, 1, 10, 1, 10, 1, 10, 1 ],
"desirableU": [ 0, 0, 0, 0 ],
"diagZ": [ 0, 0, 0, 0 ],
"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
}
],
"Simulations": [
{
"caseId": "Stabilization_1-1",
"titleSuffix": "_(1)",
"isPlotRequired": true,
"inDegrees": false,
"xInit": [ 0.3, 1, -0.4, 1, 0.2, 1, 0, 1, 0, 1, 0, -1 ]
}
]
}
The above file contains both ControlCases and Simulations arrays. The following tables explain configuration parameters for each array.
Table ControlCases Configuration
| Parameter | Possible Values | Description |
Id | string | Unique control case identifier |
isPlotRequired | true / false | Whether the plot required for this case |
logLevel | "full" / "short" / "none" | How detailed the log is |
inDegrees | true / false | Angles in degrees (true) or in radians (false) |
dt | double > 0 | Sampling interval |
N | integer > 0 | Total number of time steps |
maxIterations | integer > 0 | Number of iterations for optimization in nonlinear case |
desirableX | array of double, dimension 12 | Desirable values for the state vector (vector r) |
diagQ | array of double, dimension 12 | Values of the diagonal state weight matrix Q |
desirableU | array of double, dimension 4 | Desirable values for the open-loop system input vector (vector u) |
diagZ | array of double, dimension 4 | Values of the diagonal input weight matrix Z |
xInit | array of double, dimension 12 | Initial state xinit |
Table Simulations Configuration
| Parameter | Possible Values | Description |
Id | string | Unique simulation case identifier |
caseId | string | Correspondent control case identifiers |
isPlotRequired | true / false | Whether the plot required for this case |
inDegrees | true / false | Angles in degrees (true) or in radians (false) |
titleSuffix | string | Suffix for title of transients plot |
xInit | array of double, dimension 12 | Initial state xinit |
Standard C# configuration file App.config contains a list of appropriate case configuration JSON files and ConfigFileSelector parameter to select one of the cases for current execution. File App.config defines also RootOutputDir as the directory for output files. As it was stated above, Python code is used for generating transients plots on the fly. The absolute path to Python.exe may be defined either with Environment Variable PYTHON or, if it is not set, with parameter Python in App.config file. App.config file is presented below:
<?xml version="1.0" encoding="utf-8" ?>
<configuration>
<appSettings>
<!-- ////////////////////////////////////////////////////////////// -->
<!-- Location of the case configuration file (only one is expected) -->
<!-- Case configuration file selector -->
<add key="ConfigFileSelector" value="s1" />
<!-- Case configuration file (relative to working directory) -->
<!-- Stabilization -->
<add key="s1" value="ControlCases\Stabilization\Stabilization_1.json" />
<add key="s2" value="ControlCases\Stabilization\Stabilization_2.json" />
<!-- Transition -->
<add key="t1" value="ControlCases\Transition\Transition_1_(10, -1, 1).json" />
<add key="t2" value="ControlCases\Transition\Transition_2_(100, 10, 20).json" />
<!-- Acceleration -->
<add key="a1"
value="ControlCases\Acceleration\Acceleration_1_XY_(2, -3).json" />
<add key="a2"
value="ControlCases\Acceleration\Acceleration_2_XY_(30, -15).json" />
<!-- Deceleration -->
<add key="d1"
value="ControlCases\Deceleration\Deceleration_1_XY_(2, -3.json" />
<add key="d2"
value="ControlCases\Deceleration\Deceleration_2_XY_(30, -15).json" />
<!-- ////////////////////////////////////////////////////////////// -->
<!-- The root output directory (relative to working directory) -->
<add key="RootOutputDir" value="ControlNetOutput" />
<!-- ////////////////////////////////////////////////////////////// -->
<!-- Absolute path of Python exe file -->
<!-- <add key="Python"
value="...\AppData\Local\Programs\Python\Python310\python.exe" /> -->
</appSettings>
</configuration>
Basic Flight Modes Control
Now we will consider some basic flight modes of the copter that constitute its movement trajectory.
Stabilization
Here, stabilization means leading the copter from any current state (non-zero initial angles / angular and/or translation velocities) to the hovering state. There are no strict requirements for the final hovering point assuming that the point will be in a "certain proximity" to the initial position.
Numeric results for stabilization are given below.
Stabilization 1
This is the case of stabilization from the initial state with non-zero angles.
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 61,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0.2 | 0 | 0.2 | 0 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| diag(Q)1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| diag(Q)2 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 |
desirable u = 0,
Z = 0
Result for diag(Q)1: As it may be seen from the below transients plots, the obtained control policy stabilized the quadcopter within 5 s with displacement (x: 0.25 m, y: -0.19 m, z: 0 m) from its initial position.
 |
 |
 |
Stabilization 2
This is the case of stabilization from initial state with non-zero angles and non-zero angular and translation velocities.
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 61,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| xinit | 0.3 | 1 | -0.4 | 1 | 0.2 | 1 | 0 | 1 | 0 | 1 | 0 | -1 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| diag(Q)1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| diag(Q)2 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 | 1 |
desirable u = 0,
Z = 0
Result for diag(Q)2: The obtained control policy stabilized the quadcopter within 3 s. with displacement (x: -0.02 m, y: -0.14 m, z: 0 m) from its initial position.
 |
 |
 |
Transition
This is a transition from the initial hovering point to the final one.
In this section, we will use a value of attraction force applied to the copter (weight of the copter)
M · g = 0.65 kg · 9.81 m/s2 = 6.3765 N
Transition 1
Move the copter from initial hovering point to final hovering point (x = 10 m, y = -1 m, z = 1 m).
In this case, we define desirable state equal to the desirable final position: r7 = 10, r9 = -1 and r11 = 1.
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 101,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 0 | -1 | 0 | 1 | 0 |
| diag(Q) | 100 | 10 | 100 | 10 | 100 | 10 | 1 | 1 | 1 | 1 | 1 | 1 |
| m1 | m2 | m3 | m4 | |
| desirable u | M · g = 6.3765 | 0 | 0 | 0 |
| diag(Z) | 1 | 0 | 0 | 0 |
Result: The obtained control policy makes the quadcopter hover at the prescribed point after 8 s.
 |
 |
 |
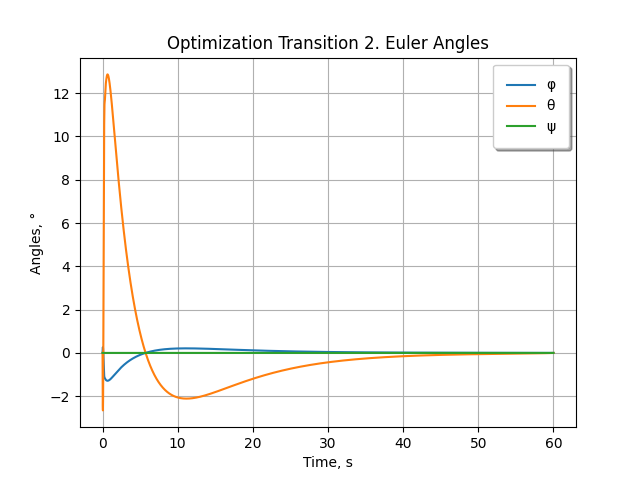
Transition 2
Move the copter from initial hovering point to final hovering point (x = 100 m, y = 10 m, z = 20 m).
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 601,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 10 | 0 | 20 | 0 |
| diag(Q) | 1000 | 1 | 1000 | 1 | 1000 | 1 | 0.01 | 1 | 0.01 | 1 | 0.01 | 1 |
| m1 | m2 | m3 | m4 | |
| desirable u | M · g = 6.3765 | 0 | 0 | 0 |
| diag(Z) | 1 | 0 | 0 | 0 |
Result: The obtained control policy makes the quadcopter hover at the prescribed point after 60 s.
 |
 |
 |
Acceleration
This is acceleration from initial hovering point to constant horizontal velocity.
Acceleration 1
Accelerate the copter from initial hovering point to horizontal velocity (dx/dt = 2 m/s, dy/dt = -3 m/s).
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 51,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | -3 | 0 | 0 |
| diag(Q) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 10 | 1 |
desirable u = 0,
Z = 0
Result: The obtained control policy makes the quadcopter move at the prescribed horizontal velocity after 3 s.
 |
 |
 |
Acceleration 2
Accelerate the copter from initial hovering point to horizontal velocity (dx/dt = 30 m/s, dy/dt = -15 m/s).
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 201,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | -15 | 0 | 0 |
| diag(Q) | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.001 | 0 | 0.001 | 10 | 0.001 |
desirable u = 0,
Z = 0
Result: The obtained control policy makes the quadcopter move at the prescribed horizontal velocity after 17 s.
 |
 |
 |
Deceleration
This is deceleration from initial constant horizontal velocity to the hovering state. This maneuver is opposite to acceleration described above.
Deceleration 1
Decelerate the copter from initial state with horizontal velocity (dx/dt = 2 m/s, dy/dt = -3 m/s) to a final hovering point (opposite to the Acceleration 1 case).
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 51,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | -3 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| diag(Q) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 | 1 |
desirable u = 0,
Z = 0
Result: The obtained control policy makes the quadcopter decelerate from its initial horizontal velocity to hovering within 5 s with displacement (x: 0.22 m, y: -0.32 m, z: 0 m) from the point where deceleration starts.
 |
 |
 |
Deceleration 2
Decelerate the copter from initial state with horizontal velocity (dx/dt = 30 m/s, dy/dt = -15 m/s) to a final hovering point (opposite to the Acceleration 2 case).
Sampling Interval Δt (in JSON configuration file - dt) = 0.1 s,
Number of Intervals N = 201,
Number of Iterations (in configuration - maxIterations) = 2.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | rad | rad/s | rad | rad/s | rad | rad/s | m | m/s | m | m/s | m | m/s |
| xinit | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | -15 | 0 | 0 |
| desirable r | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| diag(Q) | 1 | 5 | 1 | 5 | 1 | 5 | 0 | 0.01 | 0 | 0.01 | 10 | 0.01 |
desirable u = 0,
Z = 0
Result: The obtained control policy makes the quadcopter decelerate from its initial horizontal velocity to hovering within 12 s with displacement (x: 64 m, y: -27.5 m, z: 0 m) from the point where deceleration starts.
 |
 |
 |
Simulation of the application of the control policy that we just calculated to case with the same initial translation velocities, but non-zero initial angles and angular velocities. Appropriate value are provided in the table below, followed by the transients plots.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | |
| φ | dφ/dt | θ | dθ/dt | ψ | dψ/dt | x | dx/dt | y | dy/dt | z | dz/dt | |
| Units | degrees | degrees/s | degrees | degrees/s | degrees | degrees/s | m | m/s | m | m/s | m | m/s |
| xinit for optimization | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | -15 | 0 | 0 |
| xinit for simulation | 20 | -20 | 15 | -15 | -20 | 20 | 0 | 30 | 0 | -15 | 0 | 0 |
 |
 |
 |
Discussion
As we know, none of the algorithms is perfect for all cases, especially for nonlinear dynamic systems. There is no silver bullet here. Although we got some promising results for different maneuvers with a single technique, there is an endless list of possible improvements and further work.
The proposed solution implies feedback from all coordinates of the state vector (although in some modes we got some zero feedback for certain coordinates). In real-world systems, not all of them are available for direct measurements. So some well-known methods for estimation of unavailable coordinates should be used, e.g., Kalman filtering. Application of cascade control considering the closed-loop control system that we got as an internal contour may be useful to increase the robustness of the system. As a special case of the cascade control, the well-known technique of adding an integrator to the control channel may be considered. A more realistic quadcopter dynamic model should be used. The control technique may be applied in conjunction with the copter's positioning (particularly using a camera for this purpose), governance of UAV formations, etc.
LQR and ILQR may be considered as a case of Machine Learning (ML) - Model-Based Reinforcement Learning. As often in ML, computational results show features of the controlled system that can't be understood otherwise. For our quadcopter model, the sufficient number of trajectory iterations is 2. The selection of desirable vectors and weight matrices was the result of numeric experiments rather than theoretical analysis. Choice of values of weight coefficients in matrices Q and Z reflects scaling regarding desirable values. A thorough examination of discrete transfer matrices of open-loop system Fk and Hk [1](5) and the result feedback matrices LN-k and input vector of closed-loop system cN-k [1](7), where k = 0, 1, ..., N - 1 can contribute a lot to the understanding of the system dynamics. As was stated above, in some flight modes, such an analysis may suggest the decomposition of the entire dynamic system to relatively independent subsystems with a single input and feedback from only a few coordinates of the state vector x. The described technique may be used for the training of a Neural Network (NN) that generates parameters of the flight controller such as feedback gains and closed-loop system inputs.
Conclusion
This work presents the application of the technique, provided in my article [1], to a quadcopter control. Optimal in the sense of ILQR control policies are automatically generated for the flight modes like stabilization, transition, acceleration, and deceleration of the copter. Updated software generates transients plots on the fly.
History
- 17th June, 2022: Initial version
Thanks
I'd like to thank Dr. Sergey Rubinsky for useful discussions and valuable suggestions on the topic of the article.
