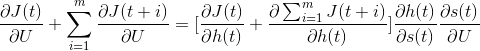ANNT: Recurrent Neural Networks
4.80/5 (17 votes)
Use of ANNT library to create recurrent ANNs and apply them to different tasks

Introduction
This article continues the topic of artificial neural networks and their implementation in the ANNT library. In the first two articles, we started with fundamentals and discussed fully connected neural networks and then convolutional neural networks. Number of sample applications were provided to address different tasks like regression and classification. This time, we'll move further in our journey through different ANNs' architectures and have a look at recurrent networks – simple RNN, then LSTM (long short-term memory) and GRU (gated recurrent unit). And again, some more examples will be provided to demonstrate application/training of recurrent networks. Some of these examples are new – something we did not do with fully connected or convolutional networks. However, some examples will address problems we've see before (like MNIST hand written digits classification), but in a different way, so results could be compared with other architectures.
Important: This article is not an introduction to artificial neural networks, but an introduction to recurrent neural networks. It is assumed that the topic of feed forward neural networks and their training with gradient descent and back propagation algorithms is well understood. If needed, feel free to review previous articles of the ANNT series.
Theoretical Background
As we've seen from the previous articles, feed forward artificial neural networks (fully connected or convolutional) can be good in classification or regression tasks when the input is represented by a single sample - feature vector, image, etc. However, in real life, we rarely operate with single samples taken out of context. Given a picture, usually we can classify it quite easily and say if there is a flower, fruit, some animal, object, etc. However, what if we are given a single image out of a video clip showing some person and asked what sort of action/gesture he is about to perform? We can make a wild guess, but in many cases we may get it wrong without looking at the video clip and getting extra context. Similar about text/speech analysis – it is really hard to guess the topic by seeing/hearing single word only. Or predicting next value of some time series based on current value only – hard to say anything without looking at the history.
This is where recurrent neural networks come into play. Like feed forward networks, those are fed one sample at a time. However, recurrent networks can build up internal history/state of what they've seen before. This makes it possible to present sequences of samples to such networks and their output will represent response not only to the current input, but response to combination of the input and the current state.
Generic block scheme of a recurrent unit is presented on the picture below. The basic idea of it is to introduce additional inputs to the unit (neuron/layer), which are connected to the outputs of the unit. This leads to extending the actual input of the recurrent unit to combination of vectors X (provided input) and H (history). For example, suppose a recurrent unit has 3 inputs and 2 outputs. In this case, the actual extended input at time t becomes a vector of 5 values: [x1(t), x2(t), x3(t), h1(t-1), h2(t-1)]. Turning this into numerical example, suppose the unit was given initial input vector X as [1, 3, 7]. This gets extended into vector [1, 3, 7, 0, 0] and the unit does its internal computations on it (unit's history is zero initialized), which may produce output vector Y as [7, 9]. The next sample given to unit is [4, 5, 6], for example, which gets extended to [4, 5, 6, 7, 9]. And so on.

The above presentation of recurrent unit is very generic though and provides simplified view of the common architectures of recurrent neural networks. Some of the architectures may have not only recurrent connection from outputs to inputs, but also maintain additional internal state of the unit. And, of course, different models differ a lot in what they do inside - very often, it goes far beyond computing weighted sums of inputs and applying activation function.
So far, the recurrent unit was presented as a black box. We briefly touched the idea of recurrent connections, but nothing was said about what are the calculations done inside the unit. Below, we are going to review some of the popular architectures of recurrent units and what sort of computations they do to provide output. Note: From now on, we'll think of recurrent units as layers in artificial neural network which can be stacked with other layers if needed.
Recurrent Neural Network (RNN)
Standard model of Recurrent Neural Network is very much similar to fully connected feed forward neural network. With the only difference that output of each layer becomes not only input to the next layer, but also to the layer itself – recurrent connection of outputs to inputs. Below is a block scheme of standard RNN, unrolled in time, so that it is seen that its output h(t) is calculated from the provided input x(t) and the history h(t-1) (output at time t-1).
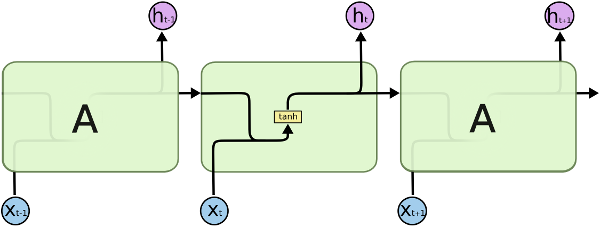
Although the block scheme above does not make it obvious, the RNN unit in it (block "A") represents a layer of n neurons, not just a single neuron. Which means as its output we get a vector h(t) of n elements. Now suppose the layer has m actual inputs (excluding recurrent ones) and so x(t) is a vector of m elements. The total number inputs then become m+n: m of the actual inputs and n of the history values. The output is then computed in the same way as for fully connected layer - weighted sums of its inputs accumulated with bias values and passed through activation function (hyperbolic tangent). Internally, the RNN layer may have a single weights' matrix of (m+n)xn size. However, to make equations clearer, it is common to assume that the layer has two weights' matrices: matrix U of mxn size used to calculate weighted sum of actual inputs and matrix W of nxn size used to calculate weighted sum of history vector. Putting this all together, results in the next equation for the output of RNN layer:
Introduction of the recurrent connection allows RNNs to connect previous information with the current input it is presented with. This means, that if analysing video stream, for example, it may classify presented video frame not only based on its content, but also taking into account previously presented video frames.
However, how far in the past RNNs can remember? In theory, these networks absolutely can handle long-term dependencies. In practice, it is very difficult to do so. As we'll see further, the difficulty of training RNNs can be caused by vanishing gradient. With multi-layer fully connected feed forward neural networks, we had a difficulty of propagating error gradient from last layers to front layers, since gradient could get smaller and smaller (vanish) while passing backward through activations. When training recurrent neural networks using Back Propagation Through Time algorithm, error gradient from processing future samples needs to be passed backward in time for processing past samples. And here, it will need to loop again and again backward through activation function.
As a result, simple RNNs may connect currently presented input with whatever was provided few steps before. However, as the gap between past and present inputs grows larger, RNNs struggle more and more to learn that connection.
Long Short-Term Memory (LSTM)
To address the issue of simple RNNs, the Long Short-Term Memory networks (LSTM) were introduced by Hochreiter and Schmidhuber in 1997, and then were popularized and refined by many other researchers. LSTM networks are a special kind of RNNs, capable of learning long-term dependencies. These networks are explicitly designed to avoid long-term dependency problem. Remembering information for long periods of time is practically default behaviour of LSTMs, not something they struggle to learn.
Unlike with simple RNNs, a single block of LSTM looks much more complex. It does considerably more computations inside and, in addition to its recurrent connection, has an internal state.

The key to LSTM is the unit's internal state (running horizontally through the top of the diagram). The unit does have an ability to remove or add information to its internal state, which is regulated by structures called gates. These gates control how much of the internal state must be kept or forgotten (removed), how much information must be added to the state and how much the state influences the final output of the unit.

The first step an LSTM unit does is deciding which information to keep in its state and which to discard. This decision is made by sigmoid block called forget gate. It takes input x(t) and history h(t-1) and produces a vector f(t) of n values in the (0, 1) range (remember, n is the size of LSTM layer's output). A value of 1 means to keep corresponding state's value as is, a value of 0 means to get rid of it completely, while a value of 0.5 means to keep half of it.

The next step of LSTM calculations is to decide which information to store in the unit's state. First, a hyperbolic tangent block creates a vector Ĉ(t) of new candidate state values, which will be added to the old state. And then, another sigmoid block called input gate generates a vector i(t) of values in the (0, 1) range, which tells how much of the candidate state to add to the old state. Same as with the previously mentioned vector f(t), both Ĉ(t) and i(t) are calculated based on the provided input x(t) and the history vector h(t-1).

Now it is time to calculate new LSTM unit's state based on the old state C(t-1), candidate state Ĉ(t) and vectors f(t) and i(t). First, the old state is multiplied (element wise) with the vector f(t), which results in forgetting some portion of the state and keeping the other. Then candidate state is multiplied with vector i(t), which chooses how much of the candidate state to take into the new state. Finally, both parts are added together, which forms the new unit's state C(t).

The last step is to decide what will be the output vector of the LSTM unit. The output of the unit is based on its current state passed through hyperbolic tangent activation. However, some filtering is done on top of it to decide which parts to output. This is done by using yet another sigmoid block called output gate, which generates a vector o(t). This one is multiplied with current state passed through activation, which forms the final output of the LSTM unit, h(t).

All the above definitely looks more complicated compared to simple RNNs. However, as you may find by playing with the provided sample applications, it does provide better result.
Gated Recurrent Unit (GRU)
There are some variants of LSTM networks, which were developed over the years. One of the variations is Gated Recurrent Unit (GRU), which was introduced in 2014 and has been growing increasingly popular since then. It does combine forget and input gates into a single update gate, vector z(t). In addition, it drops unit's internal state and operates only with the provided input and history vector. The resulting model is simpler than of the LSTM and often demonstrates better performance.

Back Propagation through Time
After proving formulas for calculating outputs of RNN, LSTM and GRU networks, now it is time to see how to train them. All variations of recurrent networks can be trained using the same stochastic gradient and back propagation algorithms, which were described in the previous articles (1st and 2nd). However, in recurrent networks the output h(t) depends not only on the provided input x(t), but also on the previous output h(t-1), which in turn depends on input x(t-1) and history h(t-2). And so on. And since we have this time dependency between outputs of the recurrent network, we need to train it keeping that dependency in mind. This results in a slight variation of the algorithm, which is reflected in its name – Back Propagation Through Time (BPTT).
When training feed forward artificial neural networks (fully connected or convolutional), training samples are presented one at a time (ignore batch training for now) – network computes its output for the given sample, cost function is calculated and then error gradient is propagated backward through the network updating its weights. When training recurrent neural networks, however, we operate with sequences instead, which are represented by a number of training samples (input/output pairs). This can be a sequence of video frames to classify, a sequence of letters/words/sounds to interpret, a sequence representing some time series values – anything where relation between current sample and past samples matters. And, since samples of a sequence have this time relation, we cannot train recurrent network using individual samples. Instead, an entire sequence must be used to calculate weights updated of the network.
And so, here is the idea of training recurrent network. We start with providing first sample of a sequence to the network, calculate output, cost value – store it along with anything required later during the back-propagation phase. Then provide second sample of the sequence, calculate output, cost value – store it all. And so on – for all samples of the sequence. Now, we should have network's outputs for each sample of the sequence and corresponding cost values calculated based on the computed output and the target output. When all samples of the sequence are provided to the network one after another, it is time to start the backward pass and calculated network's updates. Here, we start with the last sample of the sequence and go backward in time. First, weights' updates are calculated based on partial derivative of the cost J(t) with respect to the corresponding network's output, h(t). Updates are not applied though, but kept. Then we move to the previous sample at time t-1 and calculate weights' updates based on the partial derivative of the cost function for that sample, J(t-1), with respect to the output h(t-1). However, the output h(t-1) was also used to calculate the future output h(t), which affected its cost value as well. This means that at time t-1, we need not only partial derivative of J(t-1) with respect to h(t-1), but also partial derivative of J(t) with respect to h(t-1). And for the sample at time t-2, we'll need 3 partial derivative – J(t-2), J(t-1) and J(t) with respect to h(t-2). And so on.
Sounds a bit confusing you say. But, actually, it is not so. Same as with multi-layer feed forward networks, all the update rules can be derived by using the chain rule, described in the first article. To demonstrate the idea of Back Propagation Through Time algorithm, let's have a look at calculating updates of weights matrix U in RNN network. For this, we'll need to calculate partial derivatives of cost function with respect to that matrix. Below, we can see how to do that for the last sample of a sequence. Comparing it with partial derivatives we've got for fully connected feed forward network, we can see that it is exactly the same. We only changed naming of some variables, but other than that no changes. What we get here is a product of 3 partial derivative: cost function J(t) with respect to network's output h(t), network's output with respected of weighted sum of inputs/history/bias s(t) and weighted sum with respect to the matrix U. This is what chain rule did before and keeps doing well again.
We can do the same for the next training sample of the sequence at time t-1 – the sample before the last one. Looks bigger, but the same idea of the chain rule.
We can do the same one more time for yet another sample at time t-2. It all grows bigger and scarier, but hopefully shows the recursive pattern in some of the calculations.
And here it is one more time for yet another sample at time t-2. It all grows bigger and scarier, but hopefully shows the recursive pattern in the calculations.
Restructuring it a bit should make it clearer ...
Although all the above chain rules may look a bit monstrous, they are quite easy to compute when it comes to implementation. Below is the simplified version, which can be used to calculate partial derivatives of cost function with respect to matrix U for any sample of a sequence. The key here is that the sum of partial derivatives of cost functions for future samples with respect to current output is not computed again and again for every sample of a sequence. Similar to the way how error gradient propagates backward from last layer to previous layers in multilayer feed forward artificial neural network, it propagates backward through time from last sample of a sequence to the previous samples. If we take a look at the right part of the formula below, then we can notice that the part in square brackets is a sum of two partial derivatives. The first is the derivative of cost function for the current sample with respect to current output. The second is the derivative of cost functions for future samples with respect to current output. The second part of the sum is something which gets precomputed when processing future samples. So here, all we need to do is to add those two parts together and then multiply them by the last two terms following the square brackets.
We don't provide here exact formulas, but keeping them as derivatives chains for a number of reasons. First, as it was mentioned in the previous article, every term of the partial derivatives chain is represented by its own building block - like fully connected, convolutional or recurrent layer; sigmoid, hyperbolic tangent or ReLU activation function; and then different cost functions. Many of those building blocks were already discussed before and their formulas were provided. So, combining it all together should not be a big deal. And, since all these building blocks can be combined in so many ways, the resulting formula may look very different. Depending on which cost function is used, its partial derivative with respect to layer's output may look very different. More of it, pure recurrent networks are rarely the case. Very often, a neural network may have one or more recurrent layers, followed by a fully connected layer. This means that partial derivatives of cost functions with respect to the output of recurrent layer (not the final output of neural network) will get much longer. But can be derived using the same chain rule.
Anyway, let's try to complete things a bit more for the RNN network. First, we are going to add subscript k to tell that certain variable is for the kth layer of the neural network. Second, we are going to use Ek(t) to denote partial derivative of cost function for sample at time t with respect to output hk(t) – output of kth layer at time t. Also, let's use E'k(t) to denote sum of partial derivatives of cost function for all future samples (starting from time t+1 to the last sample of a sequence) with respect to output of RNN kth layer at time t, hk(t). Note that for the last sample of a sequence E'k(t=last) is 0.
This allows us to rewrite formulas for partial derivatives of cost function with respect to network parameters. Using those formulas, we can now calculate gradients for weighs matrix Uk and Wk and bias values bk, which are then plugged into standard SGD update rules (or any other, like SGD with momentum, etc.).
However, we are still missing few bits. First, we need to pass error gradient to the previous sample of the sequence, i.e. calculate E'k(t-1). And, we also need to pass error gradient to the previous layer of the network, Ek-1(t). If the network has only one single RNN layer, then Ek-1(t) calculation disappears, however.
Few more notes about training recurrent networks using back propagation through time algorithm. As it was mentioned before, when calculating gradients of network's parameters, they are not applied immediately - parameters are not updated after processing every training sample of a sequence. Instead, these gradients are accumulated. And when backpropagation phase completes for the entire sequence, those accumulated gradients are then plugged into SGD update rules (or another algorithm). What happens after processing a sequence and updating network's parameter? The recurrent state of the network is reset and then a new training sequence is processed. Resetting recurrent state means zero initializing hk(t-1) for the first sample of a sequence (no history yet) and same with E'k(t) for the last sample (no gradient from future cost yet).
Looks like this is it for training RNN with BPTT. And if something looks unclear, please remember this is not an isolated article to study on its own. Instead, it continues the topic of artificial neural networks and so it is highly recommended to visit the previous two articles as well.
As for LSTM and GRU networks, we are not going to derive formulas for their training here. Being more complicated than simple RNNs, training those looks more like a topic on its own. But, if you wish to approach those neural networks, keep in mind that one of the main things required in training them (or any other ANN architecture) is a good understand of partial derivatives and chain rule. Anyway, here are few links to get some hints (LSTM, GRU and another GRU).
The ANNT Library
Adding implementation of RNN, LSTM and GRU layers to the ANNT library was pretty much straightforward – just adding 3 more corresponding classes plus some little tweaks to make training code aware of sequences when it comes to recurrent networks. Other than that, the library kept its original structure, which was mostly laid out when implementing fully connected and convolutional artificial neural networks. Below is an updated class diagram, which did not change much since the previous article.

Same as with the rest of the library, the new classes for recurrent layers implement only their own math of forward and backward passes, i.e., compute only their own part of derivatives chain. This makes them easy to plug into existing framework and mix with layers of other types. And, following the pattern of other building blocks, the new code utilized SIMD vectorization and OpenMP parallelism whenever possible.
Building the Code
The code comes with MSVC (2015 version) solution files and GCC make files. Using MSVC solutions is very easy – every example's solution file includes projects of the example itself and the library. So MSVC option is as easy as opening solution file of required example and hitting build button. If using GCC, the library needs to be built first and then the required sample application by running make.
Usage Examples
It is time to put the theory and math aside. Instead, we'll get into building some neural networks and applying them to some tasks. Similar to what was done in the previous article, we'll have some applications which we've seen before, but approached with different artificial neural network architecture. Plus, we'll have new applications, which we did not try before. Note: None of these examples claim that the demonstrated neural network's architecture is the best for its task. In fact, none of these examples even say that artificial neural networks is the way to go. Instead, their only purpose is to provide demonstration of using the library.
Note: The code snippets below are only small parts of the example applications. To see the complete code of the examples, refer to the source code package provided with the article (which also includes examples for fully connected and convolutional neural networks described in the previous articles).
Times Series Prediction
The first example to demonstrate is time series prediction. It is exactly the same problem as we've solved with fully connected network in the first article, but now a recurrent network is used instead. The sample application trains neural network on a subset of the specified data and then uses the trained network to predict some of the data points, which were not included into the training.
Unlike with fully connected network, which has multiple inputs (depending on the number of past values used to predict the next one), the recurrent neural network has only one input. It does not mean that single value is enough to make good quality prediction though. Recurrent networks also require reasonable amount of history data. However, those are fed to network sequentially one by one and the network maintains its own history state.
As it was explained above, training recurrent network is a bit different. Since we feed values one by one and network maintains its own state, training dataset needs to be split into sequences, which are then used for training the network using back propagation through time algorithm.
Suppose a dataset with 10 values is provided:
| v0 | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 |
| 0 | 1 | 4 | 9 | 16 | 25 | 16 | 9 | 4 | 1 |
Let's assume we would like to predict 2 values and then compare prediction accuracy. This means we need to exclude 2 last values from the provided dataset (not use those for training). Finally, let's assume we want to generate sequences of 4 steps in length. This will create the next 4 training sequences:
0 -> 1 -> 4 -> 9 -> 16
1 -> 4 -> 9 -> 16 -> 25
4 -> 9 -> 16 -> 25 -> 16
9 -> 16 -> 25 -> 16 -> 9
Each of the above 4 sequences is then generates 4 training samples. For the first sequence, those sample are (x – input, t – target output):
| x | t |
| 0 | 1 |
| 1 | 4 |
| 4 | 9 |
| 9 | 16 |
Since the 4 sequences we have got are overlapping, we'll get some of the input/output training pairs repeated. However, those will be provided to the neural network with different history.
By default, the sample application creates a 2-layer neural network – first layer is Gated Recurrent Unit (GRU) with 30 neurons and the output layer fully connected with single neuron. The number of recurrent layers and their size can be overridden by using command line options, however.
// prepare recurrent ANN to train
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );
size_t inputsCount = 1;
for ( size_t neuronsCount : trainingParams.HiddenLayers )
{
net->AddLayer( make_shared<XGRULayer>( inputsCount, neuronsCount ) );
net->AddLayer( make_shared<XTanhActivation>( ) );
inputsCount = neuronsCount;
}
// add fully connected output layer
net->AddLayer( make_shared<XFullyConnectedLayer>( inputsCount, 1 ) );
Assuming training data samples are presented in the correct order (all training samples of one sequence, then all samples of another sequence, etc.) and the training context is configured with the right sequence length, the training loop becomes trivial. Note: To keep it simple, this example does not shuffle data before starting each epoch. When training recurrent networks, it is required to shuffle sequences, but not the individual training samples (which would ruin everything).
// create training context with Nesterov optimizer and MSE cost function
XNetworkTraining netTraining( net,
make_shared<XNesterovMomentumOptimizer>
( trainingParams.LearningRate ),
make_shared<XMSECost>( ) );
netTraining.SetTrainingSequenceLength( trainingParams.SequenceSize );
for ( size_t epoch = 1; epoch <= trainingParams.EpochsCount; epoch++ )
{
auto cost = netTraining.TrainBatch( inputs, outputs );
netTraining.ResetState( );
}
Output of the example application is not particularly useful other than checking cost value goes down and checking final prediction error. In addition, the example produces an output CSV file, which contains 3 columns: original data, training result (prediction of single point when providing original data as input) and final prediction (using predicted points to predict new ones).
Here are few examples of the result. The blue line is the original data we've been given. The orange line is the output of the trained network for the inputs taken from the training set. Finally, the green line represents prediction of the network. It is given data, which were not included into training set, and the output is recorded. Then the just produced output is used to make further prediction and then again.



For this particular example, recurrent network did not manage to demonstrate better result than fully connected network did. However, it was still interesting to see prediction result from using only one past value and the history maintained internally.
Sequence Prediction (One-hot Encoded)
This example application was inspired by LSTM memory example from here, but we've increased the number and length of sequences to memorize. The idea of the example is to memorize 10 slightly different sequences and then output them correctly when provided only the first digit of a sequence. Below are the 10 sequences a recurrent network needs to memorize:
1 0 1 2 3 4 5 6 7 8 1
2 0 1 2 3 4 5 6 7 8 2
3 0 1 2 3 4 5 6 7 8 3
4 0 1 2 3 4 5 6 7 8 4
5 0 1 2 3 4 5 6 7 8 5
6 0 1 2 4 4 4 6 7 8 6
7 0 1 2 4 4 4 6 7 8 7
8 0 1 2 4 4 4 6 7 8 8
9 0 1 2 4 4 4 6 7 8 9
0 0 1 2 4 4 4 6 7 8 0
The first 5 sequences are almost identical, only the first and the last digits are different. Same about the other 5 sequences, only the pattern in the middle has changed, but still the same in all those sequences. The task for a trained network is to first output '0' for any of the provided inputs, then it needs to output '1' when presented with '0', then '2' when presented with '1', and then it needs to output '3' or '4' when presented with '2'. Wait a second. How should it know what to choose, '3' or '4' if the input is the same? Yes, something fully connected network would fail to digest. However, recurrent networks have internal state (memory, so to speak). This state should tell the network to look not only at the currently provided input, but also at what was there before. And since the first digit of every sequence is different, it makes them unique. So, all the network needs to do is to look few steps behind (sometimes more than few).
To approach this prediction task, a simple 2-layer network is used - first layer is recurrent, while the second is fully connected. As we have 10 possible digits in our sequences and those are one-hot encoded, the network has 10 inputs and 10 outputs.
// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );
// basic recurrent network
switch ( trainingParams.RecurrrentType )
{
case RecurrentLayerType::Basic:
default:
net->AddLayer( make_shared<XRecurrentLayer>( 10, 20 ) );
break;
case RecurrentLayerType::LSTM:
net->AddLayer( make_shared<XLSTMLayer>( 10, 20 ) );
break;
case RecurrentLayerType::GRU:
net->AddLayer( make_shared<XGRULayer>( 10, 20 ) );
break;
}
// complete the network with fully connected layer and soft max activation
net->AddLayer( make_shared<XFullyConnectedLayer>( 20, 10 ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) );
Since each sequence has 10 transitions between digits, it will make 10 input/output one-hot encoded training samples for each. In total – 100 training samples. Those can all be fed to network in a single batch. However, to make it all work correctly, the network must be told about the length of the sequence, so that back propagation through time could do it all right.
// create training context with Adam optimizer and Cross Entropy cost function
XNetworkTraining netTraining( net,
make_shared<XAdamOptimizer>( trainingParams.LearningRate ),
make_shared<XCrossEntropyCost>( ) );
netTraining.SetAverageWeightGradients( false );
// since we are dealing with recurrent network,
// we need to tell trainer the length of time series
netTraining.SetTrainingSequenceLength( STEPS_PER_SEQUENCE );
// run training epochs providing all data as single batch
for ( size_t i = 1; i <= trainingParams.EpochsCount; i++ )
{
auto cost = netTraining.TrainBatch( inputs, outputs );
printf( "%0.4f ", static_cast<float>( cost ) );
// reset state before the next batch/epoch
netTraining.ResetState( );
}
The sample output below shows that untrained network generates something random, but not the next digit of the sequence. While the trained network is able to reconstruct all of the sequences. Replace the recurrent layer with fully connected one and it will ruin everything - trained or not, the network will fail.
Sequence prediction with Recurrent ANN
Learning rate : 0.0100
Epochs count : 150
Recurrent type : basic
Before training:
Target sequence: 10123456781
Produced sequence: 13032522355 Bad
Target sequence: 20123456782
Produced sequence: 20580425851 Bad
Target sequence: 30123456783
Produced sequence: 33036525351 Bad
Target sequence: 40123456784
Produced sequence: 49030522355 Bad
Target sequence: 50123456785
Produced sequence: 52030522855 Bad
Target sequence: 60124446786
Produced sequence: 69036525251 Bad
Target sequence: 70124446787
Produced sequence: 71436521251 Bad
Target sequence: 80124446788
Produced sequence: 85036525251 Bad
Target sequence: 90124446789
Produced sequence: 97036525251 Bad
Target sequence: 00124446780
Produced sequence: 00036525251 Bad
2.3539 2.1571 1.9923 1.8467 1.7097 1.5770 1.4487 1.3262 1.2111 1.1050
...
0.0014 0.0014 0.0014 0.0014 0.0014 0.0014 0.0013 0.0013 0.0013 0.0013
After training:
Target sequence: 10123456781
Produced sequence: 10123456781 Good
Target sequence: 20123456782
Produced sequence: 20123456782 Good
Target sequence: 30123456783
Produced sequence: 30123456783 Good
Target sequence: 40123456784
Produced sequence: 40123456784 Good
Target sequence: 50123456785
Produced sequence: 50123456785 Good
Target sequence: 60124446786
Produced sequence: 60124446786 Good
Target sequence: 70124446787
Produced sequence: 70124446787 Good
Target sequence: 80124446788
Produced sequence: 80124446788 Good
Target sequence: 90124446789
Produced sequence: 90124446789 Good
Target sequence: 00124446780
Produced sequence: 00124446780 Good
MNIST Handwritten Digits Classification
The next example is something more interesting to try – MNIST handwritten digits classification using GRU network. We already did this with fully connected and convolutional networks, so it is really interesting what recurrent networks can demonstrate on the same task. However, you may wonder where time dependency in MNIST images is. It was clear about predicting next value of a sequence (time series) based on the previous value. But here, we need to classify, not predict. And we deal with a single image. But, it all gets clear if we slightly change the task. We are not going to look at the entire image at once as feed forward networks would do. Instead, we will scan it row by row and get the classification result at the end. So instead of taking the entire 28x28 MNIST image, we are going to feed 28 rows of pixels to a recurrent network one after another. Making a correct classification of a digit by just looking at a single row of pixels is obviously impossible. But if we try to remember the other rows we've seen before, then it becomes quite doable.
The artificial neural network we going to use for this example looks pretty simple - GRU layers with 56 neurons followed by fully connected layer with 10 neurons.
// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );
net->AddLayer( make_shared<XGRULayer>( MNIST_IMAGE_WIDTH, 56 ) );
net->AddLayer( make_shared<XFullyConnectedLayer>( 56, 10 ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) );
Since we are feeding images row by row to the recurrent neural network, it is required to split each image into 28 vectors – one per each row of pixels. We then provide those sequentially to the network and use the last output as classification result. Which may look something like this:
XNetworkInference netInference( net );
vector<fvector_t> sequenceInputs;
fvector_t output( 10 );
// prepare images rows as vector of vectors - sequenceInputs
// ...
// feed MNIST image to network row by row
for ( size_t j = 0; j < MNIST_IMAGE_HEIGHT; j++ )
{
netInference.Compute( sequenceInputs[j], output );
}
// get the classification label of the image (0-9)
size_t label = XDataEncodingTools::MaxIndex( output );
// reset network inference so it is ready to classify another image
netInference.ResetState( );
Now it is time to train the GRU network and see the result:
MNIST handwritten digits classification example with Recurrent ANN
Loaded 60000 training data samples
Loaded 10000 test data samples
Samples usage: training = 50000, validation = 10000, test = 10000
Learning rate: 0.0010, Epochs: 20, Batch Size: 48
Before training: accuracy = 9.70% (4848/50000), cost = 2.3851, 18.668s
Epoch 1 : [==================================================] 77.454s
Training accuracy = 90.81% (45407/50000), cost = 0.3224, 24.999s
Validation accuracy = 91.75% (9175/10000), cost = 0.2984, 3.929s
Epoch 2 : [==================================================] 90.788s
Training accuracy = 94.05% (47027/50000), cost = 0.2059, 20.189s
Validation accuracy = 94.30% (9430/10000), cost = 0.2017, 4.406s
...
Epoch 19 : [==================================================] 52.225s
Training accuracy = 98.87% (49433/50000), cost = 0.0369, 23.995s
Validation accuracy = 98.03% (9803/10000), cost = 0.0761, 4.030s
Epoch 20 : [==================================================] 84.035s
Training accuracy = 98.95% (49475/50000), cost = 0.0332, 39.265s
Validation accuracy = 98.04% (9804/10000), cost = 0.0745, 7.464s
Test accuracy = 97.79% (9779/10000), cost = 0.0824, 7.747s
Total time taken : 1864s (31.07min)
As we can see from the above, we get 97.79% accuracy on the test set. Yes, did not manage to beat convolutional network, which gave us 99.01%. But the fully connected network with 96.55% just lost. Well, we are not going to say which network is better or worse. The tested networks have different architectures, complexity, etc. and we did not try finding the best possible configuration of those. But still, it is nice to see recurrent network classifying images well enough by looking at one row of pixel at a time and maintaining its own memory of the past.
Generating Names of Cities
To complete the demo of recurrent artificial neural networks, let's try getting some fun. The final example attempts to generate some names of cities – random, yet sounding more or less naturally. For this, a recurrent artificial neural network is trained using a dataset of US cities. Each city name is represented as a sequence of characters and the network is trained to predict next character based on provided current character and the history of previous characters (internal state of the network). Since many of the cities' names in the dataset have contradicting sequences of characters (like "Bo" can be followed by 's' as in "Boston" or by 'u' as in "Boulder", etc), it is unlikely the network will memorize any of the names. Instead, it should pick common most frequent patterns of characters' transitions. Once the network is trained (certain number of epochs), it is used to generate new names. The network is presented with one or more random characters to start with and then its output is used to complete the new generated city name.
Each character of a word sequence is one-hot encoded - 30 characters/labels are used: 26 for 'A' to 'Z', 3 for '.', '-' and space, 1 for string terminator. As the result, the neural network has 30 inputs and 30 outputs. The first layer is GRU (gated recurrent unit) and the second layer is fully connected.
// prepare a recurrent ANN
shared_ptr<XNeuralNetwork> net = make_shared<XNeuralNetwork>( );
net->AddLayer( make_shared<XGRULayer>( LABELS_COUNT, 60 ) );
net->AddLayer( make_shared<XFullyConnectedLayer>( 60, LABELS_COUNT ) );
net->AddLayer( make_shared<XSoftMaxActivation>( ) );
The helper ExtractSamplesAsSequence() function takes care of converting vocabulary words into training sequences. For example, if the word to encode is "BOSTON", then it will generate the next training sequence (one-hot encoding is applied on top of it though):
| 0 | 1 | 2 | 3 | 4 | 5 | ... | |
| Input | B | O | S | T | O | N | ... |
| Target output | O | S | T | O | N | null | ... |
Since this example application uses batch training, each training sequence must be of the same length, which is the length of the longest word in the training vocabulary. As the result, many of the training sequences will be padded with string terminator.
// create training context with Adam optimizer and Cross Entropy cost function
XNetworkTraining netTraining( net,
make_shared<XAdamOptimizer>( LEARNING_RATE ),
make_shared<XCrossEntropyCost>( ) );
netTraining.SetAverageWeightGradients( false );
/* sequence length as per the longest word */
netTraining.SetTrainingSequenceLength( maxWordLength );
vector<fvector_t> inputs;
vector<fvector_t> outputs;
for ( size_t epoch = 0; epoch < EPOCHS_COUNT; epoch++ )
{
// shuffle training samples
for ( size_t i = 0; i < samplesCount / 2; i++ )
{
int swapIndex1 = rand( ) % samplesCount;
int swapIndex2 = rand( ) % samplesCount;
std::swap( trainingWords[swapIndex1], trainingWords[swapIndex2] );
}
for ( size_t iteration = 0; iteration < iterationsPerEpoch; iteration++ )
{
// prepare batch inputs and outputs
ExtractSamplesAsSequence( trainingWords, inputs, outputs, BATCH_SIZE,
iteration * BATCH_SIZE, maxWordLength );
auto batchCost = netTraining.TrainBatch( inputs, outputs );
netTraining.ResetState( );
}
}
To demonstrate that trained network can generate something interesting, let's first have a look at some words generate by untrained network:
- Uei-Dkpcwfiffssiafssvss
- Ajp
- Vss
- Oqot
- Mx-Ueom Lxuei-Kei-T
- Qotbbfss
- Ei-Mfkx-Ues
- Wfsssa
And here is a small list of some more interesting names of cities generated by a trained neural network. Yes, may sound unusual. But still better than "asdf".
- Bontoton
- Mantohantot
- Deranber
- Contoton
- Jontoron
- Gantobon
- Urereton
- Rantomon
- Mantomon
- Zontolen
- Zontobon
- Lentohantok
- Tontoton
- Lentomon
- Xintox
- Contovillen
- Wantobon
- Intoncon
Conclusion
Well, looks like this is it with the brief overview of some common architectures of recurrent neural networks, their training and applying to different tasks. The ANNT library got extended with implementations of simple Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) layers, as well as with additional sample applications demonstrating the usage of the library. As always, all the latest code is available on GitHub, which will be getting new updates, fixes, etc.
After the set of three articles covering the topics of fully connected, convolutional and recurrent neural networks, it seems like the basic stuff is more or less covered. The future directions for the library would be adding more optimizations and performance increase by bringing GPU support, building more complicated networks represented by graphs rather than plain sequence of layers, covering new interesting architectures like capsule networks and generative adversarial networks (GAN) and so on. We'll see how we are getting on with the list.
Links
- Recurrent Neural Networks
- Fundamentals of Deep Learning – Introduction to Recurrent Neural Networks
- Backpropagation Through Time and Vanishing Gradients
- Understanding LSTM Networks
- Understanding GRU networks
- Backpropagating an LSTM: A Numerical Example
- Deriving Forward feed and Back Propagation in Gated Recurrent Neural Networks
- GRU units
- Demonstration of Memory with a Long Short-Term Memory Network
- One Hot Encoding
- MNIST database of handwritten digits
History
- 20th December, 2018: Initial version