Semi-Prime Ordered Sequences (Part 2)
5.00/5 (8 votes)
Semi-Prime Ordered Sequences (Part 2) is the follow-on to “Exploring Computational Number Theory (Part 1)” and describes a process for ordering the semi-prime base sequences.
Note: The software for this article can be downloaded from Part 1.
Introduction
This article explains the ordering of semi-prime binary sequences over an infinite modulus domain and is an in depth compendium to the "Exploring Computational Number Theory (Part 1)". As in "Exploring Computational Number Theory (Part 1)," the use of other authors’ source materials for support in producing this article is as follows:
- "BigInteger Library" by Mihnea Rădulescu, 23 Sep 2011 at http://www.codeproject.com/Articles/60108/BigInteger-Library
- "C# BigInteger Class" by Chew Keong TAN, 28 Sep 2002 at http://www.codeproject.com/Articles/2728/C-BigInteger-Class
- "Using C# .NET User Defined Functions (UDF) in Excel" by Adam Tibi, 13 Jun 2013 at http://www.codeproject.com/Articles/606446/UsingplusC-plus-NETplusUserplusDefinedplusFuncti
- Excel-DNA Version 0.32 can be obtained from here http://exceldna.codeplex.com/releases/view/119190.
- "Performance Tests: Precise Run Time Measurements with System.Diagnostics.Stopwatch" by Thomas Maierhofer (Tom), 28 Feb 2010 at http://www.codeproject.com/Articles/61964/Performance-Tests-Precise-Run-Time-Measurements-wi
Background
In "Exploring Computational Number Theory (Part 1)" I wrote about a non-ordered way of generating prime base sequences, an alternative way of saying semi-prime binary sequences. This article presents a method for generating and ordering semi-prime binary sequence simultaneously. The study of semi-prime sequences is resource intensive. Exhibit 1 below presents time resources utilized to generate the tables used in each step of the ordering process and also as a table of contents for this article. These times were generated on a notebook computer running other applications, not on a real-time or optimized benchmark system. It is just a general reference of time and you can expect a wide variance from these times if you decide to regenerate the tables.

Calculations
The following mathematical relationships will be used throughout this article and the abridged Exhibit 2 below describes this relationship in what I will term the "pMod iMod Table".
- pBase1 = any prime integer < pBase2
- pBase2 = any prime integer > pBase1
- N = pBase2 Mod pBase1
- pMod = N – 1
- iMod = (pBase1 Mod N) Mod pMod

Notice in Exhibit 2 above that primes 2 and 3 are not used. These primes {2, 3} and the prime pairs where iMod = 0 or 1 produce trivial remainders which will be presented later in this article. Also notice the following relationship with the greatest common divisor (GCD):
- If GCD(N, iMod) != 1 then the pair {pBase1, pBase2} do not exist.
Example: N =10, pMod = 9 then x = non-existent pairs for iMod = {2, 4, 5, 6, 8}
Exhibit 3 is the "Actual High Low Table" and is generated by examining actual binary sequences.
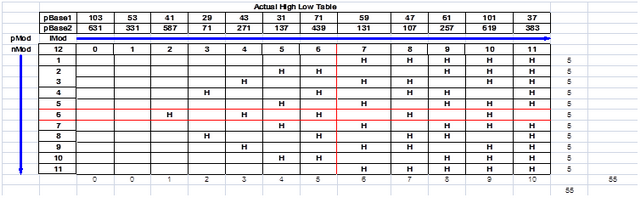
Exhibit 3 above has the following relationships:
- nMod = a number > 0 and < pMod which represents the residue increase of one within the sequence where H (high) = 1 and blank (low) = 0
- if iMod = 0 or 1 then ∑nMod = 0 per iMod
- if iMod > 1 then ∑nMod = iMod – 1 per iMod
- ∑iMod = (pMod-2-x)/2 per nMod
- ∑∑iMod = ∑∑nMod = (pMod – 1) * (pMod – 1 – x)/2
Quardrants
| iMod = 2 -> pMod – 1 (horizontal) | nMod = 1 -> pMod – 1 (vertical) |
| 1st upper left = q1 | 2nd upper right = q2 |
| 3rd lower left = q3 | 4th lower right = q4 |
| pMod odd iMod border (pMod + 1)/2 | pMod even iMod border between pMod/2 |
| nMod border between (pMod - 1)/2 | nMod border pMod/2 |
| iMod border never H because GCD(N, iMod) != 1 | iMod even then nMod set to H |
| q1 [iMod, nMod] = - q2 [N - iMod, nMod] | q2 [iMod, nMod] = - q1 [N - iMod, nMod] |
| q1 [iMod, nMod] = q3 [iMod, pMod - nMod] | q2 [iMod, nMod] = - q3 [N - iMod, pMod - nMod] |
| q1 [iMod, nMod] = - q4 [N - iMod, pMod - nMod] | q2 [iMod, nMod] = q4 [iMod, pMod - nMod] |
| q3 [iMod, nMod] = q1 [iMod, pMod - nMod] | q4 [iMod, nMod] = - q1 [N - iMod, pMod - nMod] |
| q3 [iMod, nMod] = - q2 [N - iMod, pMod - nMod] | q4 [iMod, nMod] = q2 [iMod, pMod - nMod] |
| q3 [iMod, nMod] = - q4 [N - iMod, nMod] | q4 [iMod, nMod] = - q3 [N - iMod, nMod] |

From Exhibit 4, "First Quadrant High Low Table" and subsequent tables the following relationships can be formulated:
- nMod > 0 and nMod < pMod where the number of nMod high = iMod – 1
where iMod > 1.
- If iMod even && nMod = INT(pMod / 2) then nMod = high
- If nMod even && iMod = INT(pMod / 2) then nMod = high
- if INT((1*pMod + 0) / iMod) = nMod then nMod = high
- if INT((2*pMod + 1) / iMod) = nMod then nMod = high
- if INT((3*pMod + 2) / iMod) = nMod then nMod = high
- Etcetera.
From relationship 10 above the "Calculated High Low Table" can be created. See Exhibit 5 below.

Error Detection
To check for errors in calculating the high/low table, a sequence check between the calculated and the actual can be performed. Exhibit 6 below checks the two sequences for error and has been manually modified to reflect errors as an example. Exhibit 7 below indicates the associated pMod for the error detected. 

Once the pMod where the error occurs is known (Exhibit 7), then Exhibit 8 below can be constructed to indicate the precise location of the error within the sequence.

Exhibit 9 below shows the abridged algorithmic expansion process for pMod = 29.

Algorithmic Expansion Process
Exhibit 10 below shows the algorithmic expansion process for trivial remainders where iMod < 2

Exhibit 11 below shows the abridged algorithmic expansion process for non-trivial remainders where iMod > 1

Time Cost
Exhibit 12 below indicates the cost in time of ordering the sequence while generating it. The question may be: "Why order the sequence?" One answer is "It provides a tool to study the deconstruction of semi-prime binary sequences."

Using the Code
This project was built as a concept prototype and as such does not have user friendly error checking of a more finished product. The C# code was built for a 64-bit system. Microsoft Office 2007 is a 32-bit environment requiring Excel-DNA to be compiled for 32 bits. If you want this project to run on a Microsoft Office version that is 64-bit, you will want to recompile Excel-DNA for 64 bits. The BigInterger Library has been modified for arbitrary size integers and routines from C# BigInteger Class have been used to expand the algorithms required to support this project. I have also modified the BigInteger Library with a shift divide for greater accuracy but with some loss of speed of calculation. There have been several other support routines in BigInteger Library that I have modified to expand their accuracy or to support this project. The code should be ready to go for experimenting in C# projects, Excel VBA and Excel spreadsheets. To use in Excel open BigInteger-packed.xll in a spreadsheet and there will be two function libraries, "BigInteger" and "Number Theory". A reference to BigInteger-packed.xll in the VBA environment is required for some of the macros to build the spreadsheets used in this project or to be used in other VBA applications. Microsoft Access and Excel require references to the following libraries:
- Visual Basic For Applications
- Microsoft Access 12.0 Object Library
- OLE Automation
- Microsoft Office 12.0 Access database engine Object
- Microsoft ActiveX Data Objects 6.1 Library
- BigIntExcel
If you are using .NET 4.0 or later you may want to alter this project code to use Microsoft’s Numeric library. From my research, the division algorithm is the key to accuracy and speed.
Points of Interest
This code is not thread safe because of the "RegisterSize" function which changes the values of static fields. By removing this function the process should be fairly straight forward in making this project thread safe. At present I have not explored the use of parallel processing in a multi-CPU environment. The maximum size of a BigInteger in Microsoft’s Excel 2007 is 32,767 decimal digits and will cause errors in calculations if this threshold is exceeded. See https://support.office.com/en-us/article/Excel-specifications-and-limits-16c69c74-3d6a-4aaf-ba35-e6eb276e8eaa .
History
This is the first release of this software.
