Introduction
Recently, while working on an application, I found myself needing a small polygon for use in a toolbar button. I considered using a bitmap effect to get the desired appearance, but was unsatisfied. If it was going to be necessary to put the necessary geometry into the XAML anyway, why shouldn't one put the exact XAML that was needed? Arithmetic is the problem. One of the major reasons computers are programmed is to avoid calculating numbers on spreadsheets or with a calculator.
Using the code
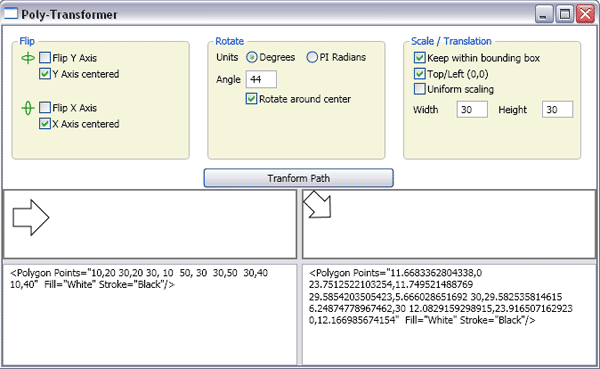
Hopefully, this code will be useful as is, even if one does not take the time to examine the source. Paste your polygon into the left hand side bottom panel. If there are no XAML parsing problems, a preview will appear above it. Select some options, and press the Transform button. The transformed XAML will appear on the right, with a preview.
How it works
The code performs the following steps:
- Extract the string containing the points, from the original XAML
- Convert the points to a matrix
- Perform the chosen calculations on the matrix
- Preview the result
Extract the string containing the points, from the original XAML
Two Regular Expressions are used to extract the points in the polygon/line.
string rString = @"(?x:
(?<PreNums><(?<Type>Polygon|Polyline).*Points\s*=\s*'\s*)
(?<Numbers>.*?\s*)
(?<PostNums>'.*)
)".Replace("'", "\"");
A second Regular Expression is used to pull out the list of coordinates.
string rMatrixString = @"(?x:
(? <x>\d+)
\s*,\s*
(? <y>\d+))";
It is worth noting that VS2008 is very loose in handling whitespace within the Points value. All the following works without problem:
Points = "1,2 3,4"Points = "1, 2 3 ,4"Points = "001,2 3, 0004"
This requires extra care in testing. The class MatrixConverter has a method FormatString that reduces the Points string to a canonical format.
Convert the points to a matrix
The string representing the points is converted into a matrix by way of the MatrixConverter.
public static Matrix Convert(string value)
{
value = FormatString(value);
string[] lines = value.Split(new string[] { " " }, StringSplitOptions.None);
Matrix m = new Matrix(lines[0].Split(new string[] { "," },
StringSplitOptions.None).Length);
try
{
foreach (string str in lines)
{
string[] line = str.Split(new string[] { "," },
StringSplitOptions.None);
Double[] newRow = new Double[m.Width];
for (int iCol = 0; iCol < m.Width; iCol++)
{
newRow[iCol] = System.Convert.ToDouble(line[iCol]);
}
m.AddRow(newRow);
}
}
catch (Exception ex)
{
throw new Exception("NonNumeric Input");
}
return m;
}
Perform the chosen calculations on the matrix
The transformations are performed in the following order: flip, rotate, scale. Also, all of the transformations implement the ITransformation interface which provides a Transform() method.
Flip transformation
The Transform method for FlipTransformation is as follows:
public void Transform()
{
double axis = 0;
if (mFlipX)
{
if (mIsXAxisCentered)
{
double min = mMatrix.Min(1);
double max = mMatrix.Max(1);
axis = (min + max) / 2;
}
else
{
axis = mXAxis;
}
FlipColumn(1, axis);
}
if (mFlipY)
{
if (mIsYAxisCentered)
{
double min = mMatrix.Min(0);
double max = mMatrix.Max(0);
axis = (min + max) / 2;
}
else
{
axis = mYAxis;
}
FlipColumn(0, axis);
}
}
public void FlipColumn(int col, double axis)
{
mMatrix.Subtract(axis, col);
mMatrix.Multiply(-1, col);
mMatrix.Add(axis, col);
}
One moves the points so that the axis one is flipping across is 0, multiplies the points by -1, and then moves them back.
Rotational transformation
The Transform method for RotateTransformation is as follows:
public void Transform()
{
double xMid =0;
double yMid = 0 ;
if (mIsRotatedAboutCenter)
{
double[] MinArray = mMatrix.MinArray();
double[] MaxArray = mMatrix.MaxArray();
xMid = (MinArray[0] + MaxArray[0]) / 2;
yMid = (MinArray[1] + MaxArray[1]) / 2;
mMatrix.Subtract(xMid,0);
mMatrix.Subtract(yMid,1);
}
switch (mRotationalUnit)
{
case ERotationalUnit.Degrees:
RotateDegreesAroundOrigin(mAngle);
break;
case ERotationalUnit.PiRadians:
RotatePiRadiansAroundOrigin(mAngle);
break;
case ERotationalUnit.Radians:
RotateRadiansAroundOrigin(mAngle);
break;
}
if (mIsRotatedAboutCenter)
{
mMatrix.Add(xMid, 0);
mMatrix.Add(yMid, 1);
}
}
public void RotateRadiansAroundOrigin(double radians)
{
Matrix mat = new Matrix(2);
mat.AddRow(new Double[2] { Math.Cos(radians), Math.Sin(radians) });
mat.AddRow(new Double[2] { -Math.Sin(radians), Math.Cos(radians) });
mMatrix.MultiplyRows(mat);
}
First, the Matrix is translated so the the origin is 0 for both the X and Y coordinates. Then, it is multiplied by the standard 2Dd transformation matrix. If you want an explanation, you could look at this.
Linear transformation
The linear transformation is a bit more involved as there are a lot of options. The basic distinction is between confining the transformation to a bounding box, or directly choosing the amount that we want to have things shifted and scaled. In that case, we can decide if we want the scaling to only affect the dimensions, but not the top and the left values. The Transform method follows. Please look at the source code for the helper methods.
public void Transform()
{
if (mBoundingBox)
{
Double currentWidth = mMatrix.Max(0) - mMatrix.Min(0);
Double currentHeight = mMatrix.Max(1) - mMatrix.Min(1);
Double ScaleX = (Right - Left) / currentWidth;
Double ScaleY = (Bottom - Top) / currentHeight;
if (mUniformStretch)
{
mMatrix.Multiply(Math.Min(ScaleX, ScaleY));
}
else
{
mMatrix.Multiply(ScaleX, 0);
mMatrix.Multiply(ScaleY, 1);
}
if (mTopLeftOrigin)
{
ShiftMinTo();
}
else
{
ShiftMinTo(Left, 0);
ShiftMinTo(Top, 1);
}
}
else
{
if (mTopLeftOrigin)
{
ShiftMinTo();
}
else
{
ShiftPlus(mShiftX, 0);
ShiftPlus(mShiftY, 1);
}
if (mUniformStretch)
{
ScaleUniform(StretchX, mFixTopLeft);
}
else
{
mMatrix.Multiply(StretchX, 0);
mMatrix.Multiply(StretchY, 1);
}
}
}
Preview the result
After the transformation is completed, the XAML is deserialized back into an object, and that object is set to the content of the previewTransformed. As this is only dealing with two classes, I opted for a simple preview.
private static void PreviewXaml(ContentControl location, string xamlString )
{
if (xamlString.IndexOf("winfx/2006/xaml/presentation", 0,
StringComparison.CurrentCulture) == -1)
{
xamlString = xamlString.Replace("/>",
" xmlns=\"http://schemas.microsoft.com/winfx/2006/xaml/presentation\" />");
}
if (xamlString.Contains("Polygon"))
{
Polygon poly = null;
try
{
poly = CreatePoly<polygon />(xamlString);
}
catch (XamlParseException ex)
{
xamlString = Regex.Replace(xamlString, "Fill=\".*?\"", "Fill=\"White\"");
xamlString = Regex.Replace(xamlString, "Stroke=\".*?\"", "Fill=\"Black\"");
poly = CreatePoly<polygon />(xamlString);
}
location.Content = poly;
}
else
{
Polyline poly = null;
try
{
poly = CreatePoly<polyline />(xamlString);
}
catch (XamlParseException ex)
{
xamlString = Regex.Replace(xamlString, "Fill=\".*?\"", "Fill=\"White\"");
xamlString = Regex.Replace(xamlString, "Stroke=\".*?\"", "Fill=\"Black\"");
poly = CreatePoly<polyline />(xamlString);
}
location.Content = poly;
}
}
Points of interest
Note that you may have trouble getting your copy of VS2008 to catch XamlParseExceptions. It appears that it may refuse even when set to do so.
I hope this is useful and saves some time from the calculator.
Written software for what seems like forever. I'm currenly infatuated with WPF. Hopefully my affections are returned.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






