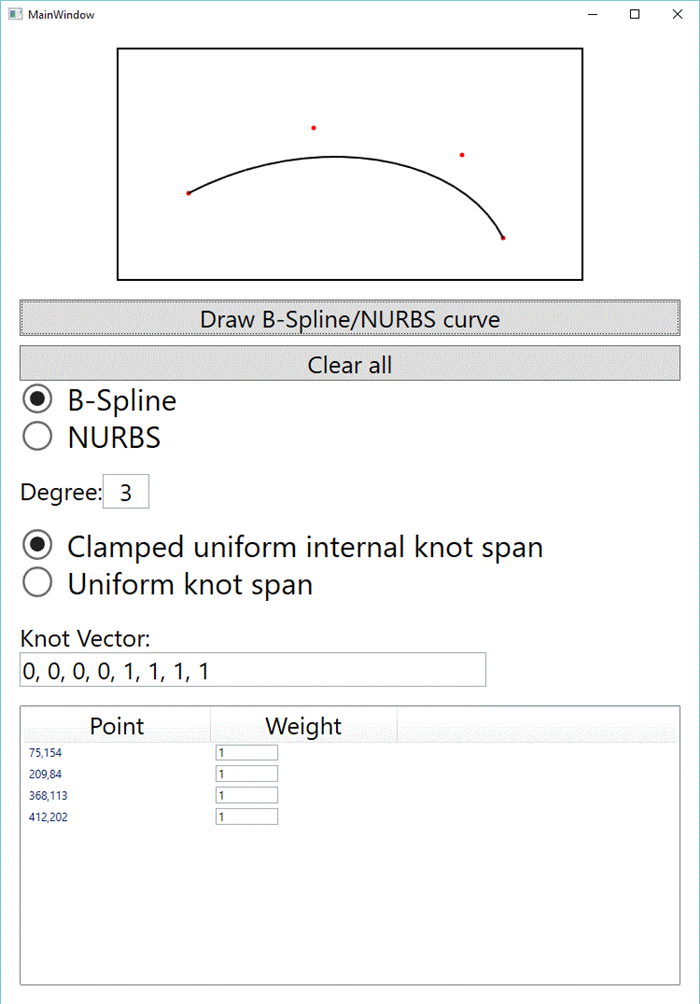
Introduction
Every time I came across a situation where I needed to create a smooth curve from some points, one item always came up, NURBS. The tutorials online where almost always way too theoretical to my liking and I had a hard time figuring out my questions about them. In general, I wanted to know two tings about them. First, how would one create them, second, how you could manipulate and use them. I was hard pressed to find any simple tutorials with a working code, that also explained what was going on.
Background
To explain the basic concepts behind the B-Spline, I will return to the Bezier curve for a moment. If you haven't already seen my articles dealing with the Bezier curve, I urge you to read it (Spline Interpolation - history, theory and implementation).
Assume that I have two points, respectively \((x_0,y_0)\) and \((x_1,y_1)\) and want to connect these with a simple line, i.a. a Bezier curve of degree 1. To blend these two I also need a value t that tells me if I'm close to the first point \((x_0,y_0)\) and I call the corresponding \(t\) value in that point for \(t_0\) and call the t value in point \((x_1,y_1)\) for \(t_1\). I also demand that the value \(t_1 > t_0\) and that the resulting function is equal to zero if it is lower than \(t_0\) and higher than \(t_1\). The most general way of writing the blending function for x and y is then:
$y(t)_{\text{$x_0$ to $x_1$}} = \frac{t_1 - t}{t_1 - t_0} \cdot y_0 + \frac{t-t_0}{t_1 - t_0} \cdot y_1 \text{ for } t \in [ t_0, t_1 ]$
The common choice for start and endpoints of the \(t\) is \(t_0 = 0\) and \(t_1 = 1\) giving a much more readable equation on the from:
$y(t)_{\text{$x_0$ to $x_1$}} = (1-t) \cdot y_0 + t \cdot y_1 $
I will later need the general form with \(t_0\) and \(t_1\) values when I want to deal with the B-Spline blending functions. You should also be aware that adding the two functions always gives:
$\frac{t_1 - t}{t_1 - t_0} + \frac{t-t_0}{t_1 - t_0} = 1$
In mathematics, this is called a convex combination of y_0 and y_1.
At the first glance it might not seem that we have gained anything by this. But lets add another point called \((x_2,y_2)\) and set up the blending formula between \((x_1,y_1)\) and \((x_2,y_2)\) :
$y(t)_{\text{$x_1$ to $x_2$}} = (1-t) \cdot y_1+ t \cdot y_2$
I can now combine the two resulting equations in a new blending function:
$y(t)_{\text{$x_0$ to $x_2$}} = (1-t) \cdot y(t)_{\text{$x_0$ to $x_1$}} + t \cdot y(t)_{\text{$x_1$ to $x_2$}}$
These three points will now be combined into a second degree piecewise polynomial Bezier curve, and the formula above can be intuitively illustrated with the following image (from Wikipedia):
There is, however, no way of controlling what degree the piecewise polynomial would have. It is simply determined by the number of points in the curve.
B-Spline
The B-Spline allows you to modulate the degree of the curve, but in order to be able to do that, it is pretty clear that you need to be able to adjust when the t's are implemented. In fact, we actually need an own vector that will hold the \(t\) values.
We would also have to place some restrictions on the knot vector, called \(U\), namely that the number of elements, \(m\), arranged as \({t_0}, \cdots , t_i , \cdots, t_{m-1}\) and the sequence must satisfy \(t_i \le t_{i+1}\). In addition, I have also chosen the interval to be \(t_0 = 0\) and \(t_{m-1}=1\). The knot span is half open meaning that the interval consists of \([u_i, u_{i+1})\) , outside this interval, as it would be if the two values are equal, the associated knot span would also be 0. Furthermore, the number of knots \(m\), the degree \(p\) and the number of control points \(n\) are connected by the formula \(n = m - p -1\).
In order to calculate the i-th B-spline function of degree p using the Cox-de Boor formula, one starts with the B-spline of 0 degrees:
$N_{i,0}(t) = \begin{cases} 1 & \text{if $t_i \le t \lt t_{i+1}$} \\[2ex] 0 & \text{otherwise} \end{cases}$
And a recursive formula that connects the lower degree with the higher degree B-Spline function is as follows:
$N_{i,p}(t)=\frac{t - t_i}{t_{i+p}-t_i}N_{i, p-1}(t) + \frac{t_{i+p+1}-t}{t_{i+p+1}-t_{i+1}}N_{i+1,p-1}$
The code for \(N_{i,p}(t)\) is then possible to construct:
private double Nip(int i, int p, double[] U, double u)
{
double[] N = new double[p + 1];
double saved, temp;
int m = U.Length - 1;
if ((i == 0 && u == U[0]) || (i == (m - p - 1) && u == U[m]))
return 1;
if (u < U[i] || u >= U[i + p + 1])
return 0;
for (int j = 0; j <= p; j++)
{
if (u >= U[i + j] && u < U[i + j + 1])
N[j] = 1d;
else
N[j] = 0d;
}
for (int k = 1; k <= p; k++)
{
if (N[0] == 0)
saved = 0d;
else
saved = ((u - U[i]) * N[0]) / (U[i + k] - U[i]);
for (int j = 0; j < p - k + 1; j++)
{
double Uleft = U[i + j + 1];
double Uright = U[i + j + k + 1];
if (N[j + 1] == 0)
{
N[j] = saved;
saved = 0d;
}
else
{
temp = N[j + 1] / (Uright - Uleft);
N[j] = saved + (Uright - u) * temp;
saved = (u - Uleft) * temp;
}
}
}
return N[0];
}
There are some special cases in the beginning and a precheck on what knot vectors that isnt 0 makes the code look a bit worse than it really is. The second for loop is where the recursive Cox-de Boor formula is implemented.
It is also possible to create a B-Spline function for any derivative of the B-Spline. I will not give the code here though, but it can be found in The NURBS book, where the code for Nip is from too.
Assuming that we have a valid knot vector and degree on the B-Spline function it is easy to generate the curve by calcualting for all t from 0 to 1:
Point BSplinePoint(PointCollection Points, int degree, double[] KnotVector, double t)
{
double x, y;
x = 0;
y = 0;
for (int i = 0; i < Points.Count; i++)
{
double temp = Nip(i, degree, KnotVector, t);
x += Points[i].X * temp;
y += Points[i].Y * temp;
}
return new Point(x, y);
}
Creating a B-Spline knot vector
The highest degree \(p\) you could have on a B-Spline curve, is actually a Bezier curve, a higher curve would not have enough control points to generate it. The knot vector for the Bezier spline is:
$U = \{ \underbrace{0, \ldots , 0}_{p+1} , \underbrace{1, \ldots , 1}_{p+1} \}$
Any lower degree, that passes trough the start point and endpoint where they are clamped (or open, sadly the terminology in literature varies), will have the general form:
$U = \{ \underbrace{0, \ldots , 0}_{p+1} , u_{p+1}, \ldots , u_{m-p-1}, \underbrace{1, \ldots , 1}_{p+1} \}$
There are many different ways that you can create a B-Spline with different coefficients in the knot vector, the only requirement is that the next value is either equal or higher than the previous one. When the knot vector is clamped it is called nonperiodic or non-uniform B-Spline, the reason beeing that the number of control point spans it includes in making the spline, will vary from 1 to the selected degree as illustrated below:

There are two methods provided to generate a knot vector in the program. One has a uniform internal knot span that is clamped in the end and beginning, and the other has a uniform knot span for all points.
private void CalcualteKnotVector(int Degree,int ContolPointCount, bool IsUniform)
{
if (Degree + 1 > ContolPointCount || ContolPointCount == 0)
return;
StringBuilder outText = new StringBuilder();
int n = ContolPointCount;
int m = n + Degree + 1;
int divisor = m - 1 - 2 * Degree;
if (IsUniform)
{
outText.Append("0");
for (int i = 1; i < m; i++)
{
if (i >= m - 1)
outText.Append(", 1");
else
{
int dividend = m-1;
outText.Append(", " + i.ToString() + "/" + dividend.ToString());
}
}
}
else
{
outText.Append("0");
for (int i = 1; i < m; i++)
{
if (i <= Degree)
outText.Append(", 0");
else if (i >= m - Degree - 1)
outText.Append(", 1");
else
{
int dividend = i - Degree;
outText.Append(", " + dividend.ToString() + "/" + divisor.ToString());
}
}
}
txtKnotVector.Text= outText.ToString();
}
The series these produce can of cource be altered to anything you'd like, but having this as a startingpoint help me very much in the beginning. You should also note that you can start with negative numbers and end on numbers higher then 1 in the knot vector, typically useful for creating polygon chapes.
Non Uniform Rational B-Splines (NURBS) curve
Once you have understood the B-Spline curve the Rational B-Spline is really simple. Each control point have a weight assigned to it, and if the weight is equal to all points, you will have the standard B-Spline curve. This gives you control of the curve around individual points without changing the degree or the controlpoint posisions, thus make the manipulation very intuitive from a human perspective. The code is really simple:
Point RationalBSplinePoint(ObservableCollection<RationalBSplinePoint> Points, int degree, double[] KnotVector, double t)
{
double x, y;
x = 0;
y = 0;
double rationalWeight = 0d;
for (int i = 0; i < Points.Count; i++)
{
double temp = Nip(i, degree, KnotVector, t)*Points[i].Weight;
rationalWeight += temp;
}
for (int i = 0; i < Points.Count; i++)
{
double temp = Nip(i, degree, KnotVector, t);
x += Points[i].MyPoint.X*Points[i].Weight * temp/rationalWeight;
y += Points[i].MyPoint.Y * Points[i].Weight * temp / rationalWeight;
}
return new Point(x, y);
}
Referances
The main resources for this article was:
- The NURBS book, 2nd Edition, by Les Piegl and Wayne Tiller
- A practical guide to Splines, by Carl de Boor
There are also some minor referances to other sites in the article where I have taken some of the images from.
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin