Solving Differential Equations: Implicit Methods

• Download source code - 859 KB

Introduction

One of the hardest things about working on mathematical calculations on the computer is IEEE arithmetical operation. Specifically, it is always an approximation to the actual solutions of the problem, regardless of the problem at hand, whether it is a differential equation or a Taylor series expansion. And how you actually control these errors is very difficult; there is no technique that can deal with every situation, even when the analytical solution is known. This often leads to ad hoc solutions that depend on multiple parameters, and the selection of a solution can also depend on the accuracy and performance you need.

In differential equations, the limit of arithmetical precision happens in so-called stiff differential equations. Under normal Runge-Kutta methods (explicit solutions), the stiff differential equation can give a solution eigenvector that goes rouge, so to speak. This simply means that rounding off errors dominates the solutions and produces the wrong results, so another method for finding the solution is desired. The explicit methods found earlier always had some issues with stability, as there was a limit that would decide when the integration schema would converge. This is referred to as the linear stability domain, where the method will give the correct solutions to the problem, and A-stability is a method that is (nearly) always stable regardless of the step size. In this domain, there is only one method that is A-stable, and that is the backwards Euler method.

In the mathematical world, there is a lot of theory that underpins the usage and stability of different methods. I will not present these here, but literature that gives more detailed explanations is given in the references. Many of the proofs are connected to matrix algebra, so it might not be so easy to follow if you haven't studied that before.

Implicit Methods

Imagine trying to solve an equation of the form:

How would you even attack this problem? We call this differential equation an implicit equation since we essentially have the same value on both sides of the equation and have no obvious method for finding a suitable solution. The general answer to how to actually find a solution is to use what is called a fixed-point iteration. The idea is in the name: you simply use a numerical approximate method that comes closer and closer to the fixed point, in layman's terms, the solution you are actually looking for, after each iteration. For finding these solutions, several mathematical methods exist, but the most widely used is the Newton-Raphson method due to its fast convergence. It is in a family of methods that can generally be constructed by a Taylor series, where the derivation comes from Stoer and Bullirsch's book "Introduction to Numerical Analysis":

This Taylor series is truncated at a certain point, for instance, at the first derivative and yields:

This will give you the classical fixed-point iteration called the Newton-Raphson root-finding method:

One can expand it to include more terms and get an even higher-order method:

which will give the following fixed-point iteration:

I have also seen this method called Schödinger's method, but there does not seem to be a general acceptance of it, at least not for now.

The problem with the higher order method is that you will get multiple roots as the solution, and you will also need the higher and higher order derivatives in order to implement higher and higher order methods.

In this article, I will stick with the simplest possible implementation so it is clear how it can be implemented. Given the derivative and a start value, one can implement the Newton-Raphson method by using the Secant method, i.e., a finite difference approximation:

public decimal CalculateImplicitStep
    (Func<decimal, decimal, decimal> df, decimal x0, decimal t, decimal dt)
{   
    // g(x) for Implicit Euler calculations
    decimal g(decimal x)  { return x - x0 - dt * df(x, t + dt); };
    
    //  g'(x) approximated with the secant method
    decimal gdot(decimal y1, decimal y0) 
       { return 1 - dt*((df(y1, t + dt) - df(y0, t+dt)) / (y1 - y0)); };
    
    // Starting point for the error
    decimal error = 1.0M;
    // Error tolerance
    decimal tol = 1e-10M;
    // Max number of iterations
    int maxIterations = 10;
    int iteration = 0;
    
    // Starting point
    decimal y0 = x0;
    // First estimate using forward Euler
    decimal y1 = x0 + dt * df(x0, t + dt);
    
    // Newton-Raphson iterations
    while (error > tol && iteration < maxIterations)
    {
        decimal y2 = y1 - (decimal)(g(y1) / gdot(y1,y0));
        error = (decimal)Math.Abs((double)(y2 - y1));
        y0 = y1;
        y1 = y2;
        iteration++;
    }
    
    // Return estimate within range or from max number of iterations
    return y1;
}

The real strength of the implicit method is that it is stable for nearly all values of dt, and those timesteps that are not valid can be calculated from the equations a priori (in advance), which none of the explicit methods can do.

To use the Newton-Raphson method, a function that is set equal to zero is needed. Here, the forward Euler method is used for the function:

Moving everything over and setting it equal to zero:

A simple implementation of the method like I showed is not generally recommended since the Newton-Raphson method might not converge to a single value for all functions. Given this fact, a general root-finding method is usually implemented instead. One usually starts with the highest-order method, since this will converge to the solution the fastest. And if that method fails, one simply makes use of a lower-order method. Once all other methods fail, the last and most surefire method, and by far the slowest, is the bisection method, which is used as a last resort.

One often-used implementation of a general and reliable root-finding algorithm is what's called Brent's method. Details on this implementation can be found on Cleve Moler's blog. In short, it combines three methods: the Newton-Rapson implementation with the secant method, the inverse quadratic interpolation method (with three points) used to find a better approximation for the zero crossing point, and at last, the bisection method.

The Newton-Raphson method with the analytical derivative has a degree 2 convergence, but that is usually a bit cumbersome to implement as a general method since it is often not known in advance. Using the secant method eliminates this necessity by implementing the derivative as a finite difference instead, but this comes at a cost since the secant method has a super linear convergence of 1.6 order. But it is way better than the bisection method, which has linear convergence of order 1. For the sake of clarity, a degree 2 method will improve the approximation by two decimal points per iteration, and a degree 1 method will improve the approximation by one decimal point per iteration.

Practical Example

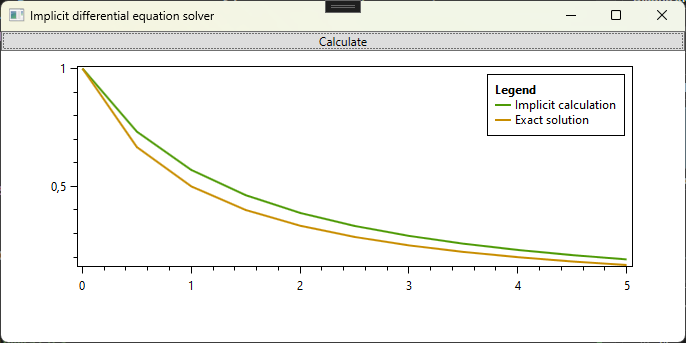
So here is a simple example of how to use the implicit method to solve a simple differential equation:

This example is taken from the Wikipedia article, and as can be seen, the implementation given in my code makes identical graphs to the Wikipedia article.

The code that implements the differential equation and its exact solution are given:

/// <summary>
/// The differential equation y' = -y^2
/// </summary>
/// <param name="y"></param>
/// <param name="t"></param>
/// <returns></returns>
public decimal ydot(decimal y, decimal t)
{
    return -y * y ;
}

/// <summary>
/// Exact solution to y' = -y^2
/// </summary>
/// <param name="t"></param>
/// <returns></returns>
public decimal ExcactSolution(decimal t) 
{
    return 1 / (InitialValue + t);
}

Future Work

This article was just a stepping stone to a complete implementation of the Butcher-Tableau, where we are now aiming to combine explicit and implicit methods like the classical Crank-Nicolson implementation, which combines one explicit step with an implicit step, and this is an example of an IMEX scheme (implicit-explicit).

History

• 2^nd January, 2024: Initial posting