Introduction
Although the usefulness of STL containers is undeniable, they also come with their set of limitations. Evolving in the speech recognition industry myself, and having to deal with often huge amount of data, the most obvious limitation introduced by STL containers is the fact that all the data needs to reside in memory.
In the context of dictation speech recognition software, most speech recognition engines require ARPA compliant language models to perform their magic. Just imagine the task of building a language model from hundreds of megabyte of corpus data, and, in the process, getting to the determination of probabilities of not only words, but also sequences of words. Such a task is almost impossible with the exclusive use of unmanaged STL containers.
In the present article, I will expose a solution to that problem and use the opportunity to also introduce you to the wonderful world of speech recognition (or at least a portion of it) by going over the code that can handle the generation of an ARPA compliant language model from hundreds of megabytes of corpus data without ever running out of memory.
Background
ARPA compliant language models have been around for quite some time, and they are not going anywhere in the foreseeable future. They are the primary means by which a speech recognition engine can be dictated how to bias its speech input and recognize textual data as a result. Although a general English language model obviously achieves a purpose, the tendency has diverted in the previous years to generate more specialized language models. For example, a radiology language model could be used in the Medical field where practicians historical corpus of data would be used to generate an highly specialized model, hence minimizing false-recognition since the vocabulary would be more constrained.
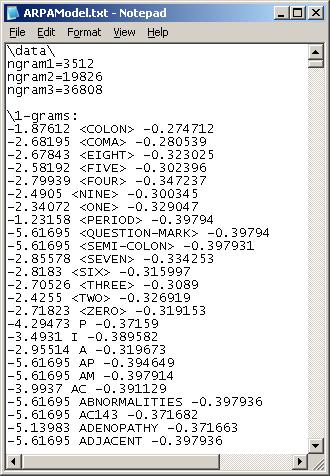
Here is an actual language model for us to look at. It comes from the following corpus of text:
This is a test
This is a second test
With a fixed discounted mass of 0.4 (more on that later), the trigram (limited to sequences of 3 words) language model generated from that limited corpus of text is as follows:
\data\
ngram 1=5
ngram 2=5
ngram 3=4
\1-grams:
-0.8751 This -0.3358
-0.8751 a -0.3010
-0.8751 is -0.3358
-1.1761 second -0.3358
-0.8751 test -0.3979
\2-grams:
-0.2218 This is 0.0000
-0.5229 a second 0.0000
-0.5229 a test. -0.3979
-0.2218 is a 0.0000
-0.2218 second test -0.3979
\3-grams:
-0.2218 This is a
-0.2218 a second test
-0.5229 is a second
-0.5229 is a test
\end\
On the left side of each sequence of words is the probability, and on the right side is the backoff probability (except for the 3-grams). Here's how it works. For example, let's take the line "-0.8751 This -0.3358".
Let's start simple. The probability of the word "this" in the corpus of text is 2/9 (there are 2 occurrences of the word "this" over a total of 9 words) multiplied by 0.6 (1 - 0.4, the non-discounted mass). The number that is required in the ARPA compliant language model is the actual log of that calculation. Hence, log(2/9 * (1 - 0.4)) = -0.8751.
A little word is required about discounts and backoff probabilities. Backoff probabilities are related to non-terminated utterances. For example, if I'd be talking, I could well say something like "this is a" and later continue "test". Without backoff probabilities, a speech recognition engine would fail at recognizing the non-terminated utterance since it would not have any probability associated with it. For that simple reason, and since a probability always needs to sum to one, we take a chunk of the probability mass (the discount of 0.4 in our case) and reserve it for backoff probabilities. Since the model is a trigram, you will understand that the 3-grams do not have any backoff probabilities associated with them.
Consequently, here is how the backoff probability of "this" is calculated. The sum of all the N-gram probabilities completing the (N+1)-grams of words starting with the N-Gram word is computed, and it is then diluted the discount mass and log. For the case of "this", that means log(0.4/(1-0.13332)) since the only 2-gram sequence starting with "this" is "this is" and that the probability of "is" is 0.133332 (10 exp -0.8751).
When calculating N-grams where N>1, instead of dividing the count of sequences of words by the total amount of sequences of words, the count is divided by the count of (N-1)-grams starting with the same sequence of words. For example, the probability related to "this is" is log(2/2 * (1 - 0.4)) = -0.2218 since there are 2 occurrences of the word "this" as well as 2 occurrences of the sequence "this is".
These calculations are not so complex, but nevertheless, since there are so many dependencies between the count generating the probabilities and then the backoff probabilities requiring the previous determination of other corresponding probabilities, it is impossible to perform the calculations before all the data is organized and in place. The problem of generating a language model is an indexing problem more than anything else. That is, the algorithm needs to keep track of many counts of many words and sequences of words prior to starting any calculation. I will expose here how that can be done with STL containers without ever running out of memory regardless of the fact that hundreds of megabytes of data could be processed.
Using the Code
Step 1 (Optional): Garbage Collection
To start our task, we will first create a garbage collection template. Although we could have achieved our goal without it, I find it cleaner to create a garbage collection logic and build upon it than to have to mingle with deletes all over the place.
The std::auto_ptr template is almost perfect for garbage collection, but it lacks a copy constructor and assignment operator. For that reason, I propose the shared_auto_ptr as following. I create a contained_auto_ptr template class that has for purpose to hold a unique pointer address that was referred to by a shared_auto_ptr object. That template class is private and only shared_auto_ptr should ever use it. Its copy constructor and assignment operators are private to ensure they are not mis-manipulated by anyone else. The shared_auto_ptr is composed of one pointer to a contained_auto_ptr that holds the count referring to it. The constructor, destructor, copy constructor and assignment operators of the shared_auto_ptr are all written so that count from the associated contained_auto_ptr object is maintained accordingly, and once the count gets down to zero, the associated memory to the contained_auto_ptr object, as well as the contained_auto_ptr itself are deleted. As long as the user of that interface disciplines herself/himself not to use any pointers anywhere else in the code, this is a bullet-proof garbage collection methodology with only little overhead.
template <class T> class contained_auto_ptr
{
public:
friend class shared_auto_ptr<T>;
protected:
static contained_auto_ptr<T> *GetContainer(T* p = NULL) throw();
T *get() const throw();
~contained_auto_ptr() throw();
private:
contained_auto_ptr(T* p = NULL) throw();
static map<uintptr_t, contained_auto_ptr<T>*> m_equivalenceMap;
contained_auto_ptr(const contained_auto_ptr&) throw();
void operator=(const contained_auto_ptr&) throw();
int m_count; T *_ptr; };
template <class T> class shared_auto_ptr
{
public:
shared_auto_ptr(T* p = NULL) throw();
~shared_auto_ptr() throw();
shared_auto_ptr(const shared_auto_ptr&) throw();
void operator=(const shared_auto_ptr&) throw();
T *get() const throw();
T *operator->() const throw() { return get(); }
private:
contained_auto_ptr<T> *m_contained_auto_ptr;
};
With the implementation of this template as included in the code, I can now abstract my dealings with pointers and forget about the deletes. That results in simpler and more reliable code.
Step 2: An Indexing Strategy
Typically, if I'd abstract my memory concerns, a std::map<string,struct> would be the perfect candidate to resolve my indexing problem. But, with my memory concerns, the std::map template becomes useless. It needs to be replaced by another structure that acquires the same qualities as the std::map template, but becomes more versatile when it comes to memory management.
For that purpose, I have chosen a 3-way decision tree. An example of the decision tree, populated with 2 entries, looks like the following:
IndexStructure<int> tree;
tree["this"] = 3;
tree["test"] = 2;
t(NULL)
/|\
/ | \
/ | \
/ | \
/ | \
/ | \
/ h(NULL)\
NULL /|\ NULL
/ | \
/ | \
/ | \
/ | \
/ | \
e(NULL)| NULL
| is(3)
|
st(2)
The decision tree has a head node, and each node is composed of a reference to a smaller than node, an equal to node and a greater than node. The indexing strategy is not revolutionary on its own, but it gets the job done.
template <class T> class IndexStructureNode
{
public:
friend class IndexStructure<T>;
friend class IndexStructureIterator<T>;
~IndexStructureNode() throw();
protected:
IndexStructureNode(const IndexStructureNode<T> ©) throw();
IndexStructureNode<T> &operator=(const IndexStructureNode<T> ©) throw();
unsigned long GetNodeId() const throw() { return m_nodeId; }
T *get() const throw() { return m_data.get(); }
IndexStructureNode(IndexStructure<T> &owner, bool assignId = true) throw();
static IndexStructureNode<T> *ReadNode(IndexStructure<T> *owner,
fstream &dStream, unsigned long dNodeId) throw(fstream::failure);
void ReadNodeData(fstream &dStream) throw(fstream::failure);
void WriteNode(fstream &dStream) throw(fstream::failure);
void WriteNodeData(fstream &dStream) throw(fstream::failure);
string GetKey() throw();
inline void SetDirty() throw();
inline void FlagReference() throw();
private:
unsigned long m_nodeId; string m_index; mutable unsigned long m_lastAccess; unsigned long m_parentNode; unsigned long m_equalChildNode; unsigned long m_smallerChildNode; unsigned long m_greaterChildNode; shared_auto_ptr<T> m_data; IndexStructure<T> &m_owner; bool m_dirty; };
With the IndexStructureNode template defined, the IndexStructure becomes definable as follows:
#define MEMORYMAP(T) std::map<unsigned long, shared_auto_ptr<IndexStructureNode<T> > >
template <class T> class IndexStructure
{
public:
friend class IndexStructureNode<T>;
friend class IndexStructureIterator<T>;
IndexStructure(unsigned int nodeDataLength, unsigned int nodeIndexLength = 6,
unsigned int maxNodesInMemory = 2000) throw(FileErrorException,
fstream::failure);
~IndexStructure() throw();
unsigned long GetNodesCount() const throw() { return m_nodesCreationCount; }
unsigned long GetNodesInMemoryCount() const throw()
{ return m_memoryNodes.size(); }
bool HasData(const string index) throw();
T& operator[] (const string index) throw(AlgorithmErrorException);
void PurgeFromMemory() throw();
protected:
shared_auto_ptr< IndexStructureNode<T> >
AdaptNodeIndexSize(shared_auto_ptr< IndexStructureNode<T> > &node) throw();
shared_auto_ptr<IndexStructureNode<T>> LoadNode(unsigned long dNodeId)
throw(BadNodeIdErrorException, fstream::failure);
void WriteHeader(fstream &dStream) throw(fstream::failure);
void SeekStreamToNodePosition(fstream &dStream, unsigned long dNodeId)
throw(fstream::failure);
void AdaptParentsInChildNodes(shared_auto_ptr< IndexStructureNode<T> >
&dNode) throw();
private:
string m_fileName;
unsigned int m_nodeIndexLength;
unsigned int m_nodeDataLength;
unsigned int m_maxNodesInMemory;
fstream m_cacheStream;
mutable unsigned long m_nodesCreationCount;
mutable unsigned long m_accessCount;
mutable MEMORYMAP(T) m_memoryNodes;
mutable int m_headerSize;
mutable unsigned long long m_lastAccessTotal;
static const char *m_zeroBuffer;
};
The important things to note are the presence of m_memoryNodes, m_lastAccess and m_maxNodesInMemory. m_memoryNodes is the std::map that is not optimized for intensive memory usage, and m_maxNodesInMemory specifies how many nodes could be in memory at any given time. m_lastAccess holds a value that was assigned sequentially so that we could later determine how old an access to that IndexStructureNode was made (we will want to keep in memory the latest referenced nodes, and dispose of the older ones at purge time). It is important for each IndexStructureNode to be serializable for the IndexStructure to cache to disk.
While maintaining the m_lastAccess in each IndexStructureNode object, I also maintain m_lastAccessTotal into the associated IndexStructure object. That will keep the total so that I could later use it to average and get to a determination if a reference to a single IndexStructureNode is old enough to be purged or not.
For the caching to disk to be efficient, it helps if the size of a IndexStructureNode object to disk is predictable since we could simply offset its location in a file by a calculation dependant of its id. Once that is all in place, a periodic purge of the memory is invoked as follows:
template <class T> void IndexStructure<t>::PurgeFromMemory() throw()
{
if (m_memoryNodes.size() > m_maxNodesInMemory)
{
MEMORYMAP(T) swapMap;
unsigned long long newTotal = 0;
WriteHeader(m_cacheStream);
unsigned long avgAccess = (unsigned long)
(m_lastAccessTotal/m_memoryNodes.size());
avgAccess += (avgAccess/3);
{
for (MEMORYMAP(T)::iterator it = m_memoryNodes.begin();
it != m_memoryNodes.end(); it++)
{
if (it->second.get()->m_lastAccess < avgAccess)
{
it->second.get()->WriteNode
(m_cacheStream);
it->second = NULL;
}
if (it->second.get() != NULL)
{
newTotal += it->second.get()->
m_lastAccess;
swapMap[it->first] = it->second;
}
}
}
m_memoryNodes = swapMap;
m_lastAccessTotal = newTotal;
}
}
... and one needs to always call a special method that will populate a node in memory in the event that it is cached to disk, implemented as follows:
template <class T> shared_auto_ptr<IndexStructureNode<T>>
IndexStructure<T>::LoadNode(unsigned long dNodeId)
throw(BadNodeIdErrorException, fstream::failure)
{
if (m_memoryNodes.find(dNodeId) != m_memoryNodes.end())
{
return m_memoryNodes[dNodeId];
}
else
{
if ((dNodeId > m_nodesCreationCount) || (dNodeId < 1))
{
throw(BadNodeIdErrorException("Bad node id."));
}
IndexStructureNode<T> *dNewNode =
IndexStructureNode<T>::ReadNode(this, m_cacheStream, dNodeId);
m_memoryNodes[dNodeId] = shared_auto_ptr
<IndexStructureNode<T>>(dNewNode);
return m_memoryNodes[dNodeId];
}
}
The indexing strategy would not be completed without some mechanisms to iterate through the accumulated data. For that purpose, the IndexStructureIterator template class was created.
template <class T> class IndexStructureIterator
{
public:
friend class IndexStructure<T>;
friend class IndexStructureNode<T>;
IndexStructureIterator(IndexStructure<T> &structure) throw();
IndexStructureIterator<T> operator++(int) throw();
T *get() const throw();
void Reset() throw();
void Reset(IndexStructureIterator<T> &it) throw();
bool End() throw();
string GetKey() throw();
IndexStructureIterator<T> Begin() throw();
private:
class CDecisionOnNode
{
public:
enum EDirection
{
goLeft = -1,
goCenter = 0,
goRight = 2,
goUp = 3
};
CDecisionOnNode(unsigned long dNodeId, EDirection dDirection):
m_nodeId(dNodeId), m_direction(dDirection) {}
unsigned long m_nodeId;
EDirection m_direction;
};
IndexStructureIterator<T> &operator++() throw() {}
void IterateToNextPopulatedNode() throw();
stack<CDecisionOnNode> m_decisions;
IndexStructure<T> &m_structure;
bool m_endReached;
shared_auto_ptr< IndexStructureNode<T> > m_curNode;
};
The iteration through the tree uses a stack of CDecisionOnNode in order to ensure that each node is only visited once. By maintaining that stack of CDecisionOnNode, the algorithm already produces an answer to a later inquiry (where should I go), and the size of the stack is limited to the depth of the index tree. The algorithm looks as follows:
template <class T> void IndexStructureIterator<T>::IterateToNextPopulatedNode() throw()
{
shared_auto_ptr< IndexStructureNode<T> > disqualifyNode = m_curNode;
if ((!m_endReached) && (!m_decisions.empty()))
{
bool skipNextTest = false;
do
{
CDecisionOnNode dDecision = m_decisions.top();
if (dDecision.m_nodeId != m_curNode->GetNodeId())
{
CDecisionOnNode otherDecision
(m_curNode->GetNodeId(), CDecisionOnNode::goLeft);
if (m_curNode.get()->get() != NULL)
{
m_decisions.push(otherDecision);
break;
}
else
{
dDecision = otherDecision;
m_decisions.push(otherDecision);
}
}
switch (dDecision.m_direction)
{
case CDecisionOnNode::goLeft:
m_decisions.top().m_direction =
CDecisionOnNode::goCenter;
if (m_curNode->m_smallerChildNode != 0)
{
m_curNode = m_structure.LoadNode
(m_curNode->m_smallerChildNode);
}
else
{
continue;
}
m_decisions.push(CDecisionOnNode
(m_curNode->GetNodeId(),
CDecisionOnNode::goLeft));
break;
case CDecisionOnNode::goCenter:
m_decisions.top().m_direction =
CDecisionOnNode::goRight;
if (m_curNode->m_equalChildNode != 0)
{
m_curNode = m_structure.LoadNode
(m_curNode->m_equalChildNode);
}
else
{
continue;
}
m_decisions.push(CDecisionOnNode
(m_curNode->GetNodeId(),
CDecisionOnNode::goLeft));
break;
case CDecisionOnNode::goRight:
m_decisions.top().m_direction =
CDecisionOnNode::goUp;
if (m_curNode->m_greaterChildNode != 0)
{
m_curNode = m_structure.LoadNode
(m_curNode->m_greaterChildNode);
}
else
{
continue;
}
m_decisions.push(CDecisionOnNode
(m_curNode->GetNodeId(),
CDecisionOnNode::goLeft));
break;
case CDecisionOnNode::goUp:
m_decisions.pop();
if ((m_curNode->m_parentNode != 0)
&& (!m_decisions.empty()))
{
m_curNode = m_structure.LoadNode
(m_curNode->m_parentNode);
disqualifyNode = m_curNode;
}
else
{
m_endReached = true;
}
break;
}
}
while ((!m_endReached) && ((m_curNode.get()->get() == NULL) ||
(disqualifyNode.get()->get() == m_curNode.get()->get()))
&& (!m_decisions.empty()));
}
if (m_curNode.get()->get() == NULL)
{
m_endReached = true;
}
}
Step 3: Putting It All Together into a Language-Model Calculation Class
The creation of a language-model generation class (CLMEngine) becomes easy once these services are in place. As a matter of fact, the CLMEngine class's implementation fits within 150 lines of code (with almost 1/3 being comments), and the logic is extremely easy to follow. Even better than that is the fact that its calculations are never bound to any memory limitation issues.
double CLMEngine::CalculateOneProbability(string dKey, CNodeData dNodeData) throw()
{
if (dNodeData.m_level == 1)
{
return (double)((double)1.0-m_discount) *
(double)dNodeData.m_count/(double)m_levelEvents
[dNodeData.m_level-1].m_events;
}
else
{
return (double)((double)1.0-m_discount) *
(double)dNodeData.m_count/(double)m_index
[dKey.substr(0, dKey.length() -
dNodeData.m_lastTokenLength - 1)].m_count;
}
}
double CLMEngine::CalculateOneBackoffProbability
(IndexStructureIterator<cnodedata> &dLocationInTree) throw()
{
double dSum = 0;
IndexStructureIterator<cnodedata> it(m_index);
for (it.Reset(dLocationInTree); !it.End(); it++)
{
if ((it.get()->m_level == (dLocationInTree.get()->m_level + 1)) &&
(dLocationInTree.GetKey().compare(it.GetKey().substr(0,
it.GetKey().length() - it.get()
->m_lastTokenLength - 1)) == 0))
{
string dKey = it.GetKey().substr
(it.get()->m_firstTokenLength + 1);
dSum += CalculateOneProbability(dKey, m_index[dKey]);
}
}
return (m_discount/(floor(((double)1-dSum)*100000+0.5)/100000));
}
Points of Interest
With the code attached to this article, a language-model is generated from a corpus of 1.5 MB within 2 minutes of analysis time.
Note that the IndexStructure class could be improved to be written and read to and from disk. That would be somewhat useful in order to skip the word counting phase within the context of language-model calculation and would allow for a faster merge of multiple language-models. To this day, merging language models has almost never been factored into research and even less deployments. Now that we are heading towards more specialization of language-models, one could easily think of a physician that is a radiologist and an oncologist. He could be offered to use a language-model that holds both corpus at the same time, and for these calculations to happen, if the count files would have been kept to disk, the merging process only becomes a matter of generating a sum index tree and then performing the language-model calculations themselves (hence saving a lot of time on recounting the words once again).
That being said, for those that are not as passionate about speech-recognition as I am, I hope the exposed techniques to deal with memory management within this article would benefit some in the community that has given me so much over time.
History
- Wednesday, December 10th, 2008: Article created
Philippe Roy was a key contributor throughout his 20+ years career with many high-profile companies such as Nuance Communications, IBM (ViaVoice and ProductManager), VoiceBox Technologies, just to name a few. He is creative and proficient in OO coding and design, knowledgeable about the intellectual-property world (he owns many patents), tri-lingual, and passionate about being part of a team that creates great solutions.
Oh yes, I almost forgot to mention, he has a special thing for speech recognition and natural language processing... The magic of first seeing a computer transform something as chaotic as sound and natural language into intelligible and useful output has never left him.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







 Nicholas,
Nicholas,