The dependant.zip or dependant.rar is the environment for building testing application running on Windows, to know more in detail, please refer to readme.txt in compressed file redistribution.rar or redistribution.zip.
Introduction
The algorithm introduced in this tip and provided in C++ code has time complexity of O(N*LogN), the basic idea is from here, sweepling line is pivotal, and sweepling line enables computer vision for triangulating the polygon. In addition, this algorithm provides a solution for self-intersected polygon and with correspondingly 2 ways of triangulation, one for even-odd fill mode, the other is for winding fill mode. For more details, please refer to libtriangulation.h.
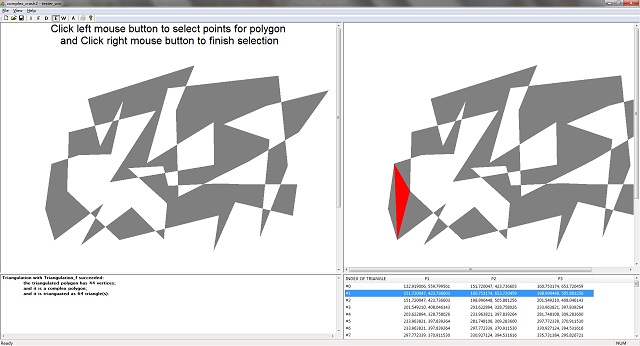
The image above shows the testing application of this algorithm running on Windows, all the testing functions can be initivated by the buttons on the toolbar, buttons marked as "I", "F", "D" are for testing triangulation algorithms corresponding to data type of "integer", "float", "double" respectively, button marked as "E" and "W" are for setting the fill mode to be "even-odd" and "winding" respectively. Lastly, button marked as "A" is for initiating a built-in case test. To use this application: Firstly, use mouse to create a polygon, Secondly, set the fill mode with button either marked as "E" for even-odd or marked as "W" for winding, thirdly press button "I", "F" or "D" to run the triangulation algorithm with polygon input generated by mouse and with preset fill mode, then in the left view, it draws the expected filled polygon and in the right it draws the triangles generated by the algorithm; the left view is painted by GDI, and the right view is painted by OpenGL, since the coordinate system of OpenGL supports floating points, therefore it can sufficiently test on this algorithm. when an item in the list view is selected, then the corresponding triangle will be highlighted in red. Technically, this algorithm supports all the signed number data type, however, practically it works the best with the maximum precise data type----double type. By comparison of the left and right view optically, we can confirm if the algorithm works correctly.
Background
Polygon triangulation is an important topic in 2d computer graphics, working with triangles is more convenient than working with various kinds of polygons, as an extension triangle also defines a plane, therefore it is geometrically significant for 3d graphic engines, furthermore the OpenGL and direct3d are making triangle as one of their graphical primitives. Motivation of this algorithm is for optimizing the polygon rending by utilizing the graphical hardware, hence OpengGL is one of the options, using this algorithm triangulates the polygon, and generates the triangles, and then send the triangles away to the graphical hardware with OpenGL, to maximally utilize the graphical hardware. The interface of the algorithm is designed seamlessly for graphical engine, with 2 types of polygon fill-mode supported, one is Even-Odd, the other is Winding. For more information about these 2 types of filling mode, you can refer to this link for winding, and this link for even-odd.
Using the Code
The triangulation algorithm is wrapped in a standalone dynamic link library, the interface of the library is defined in file libtriangulation.h ($Package\libtriangulation\triangulation\src\libtriangulation.h). Using the library can be depicted in the following pseudo code:
Polygon2D_f polygon;
Triangles_f *triangles = NULL;
polygon.num = 3
polygon.points = new Point2D_f[3];
polygon.points[0].x = 0;
polygon.points[0].y = 0;
......
if (GenerateTriangles_f(&polygon, Even_Odd, &triangles) > 0)
{
for (unsigned int i_tri = 0; i_tri < triangles->num; i_tri ++)
{
const Point2D_f &pt1 = triangles->pts[i_tri][0]; const Point2D_f &pt2 = triangles->pts[i_tri][1]; const Point2D_f &pt3 = triangles->pts[i_tri][2]; }
ReleaseTriangles_f(triangles);
}
delete [] polygon.points;
polygon.points = NULL;
polygon.num = 0;
For more information about how to use the library through the interface, please refer to ListPoints_i.h, ListPoints_i.cpp (in folder tester_win), particularly to function CListPoints_i::GenPolygon_f, this function converts the MFC list of points to Polygon2D_f; or the file mock_vega.h, mock_vega.cpp, cases.h which works on linux.
It's recommended to use tester_win to learn, test, and evaluate the algorithm; tester_win runs on Windows 7.0 with OpenGL 3.0 minimally. Once the algorithm works abnormally (comparing the left view and right view, it has obvious difference), then save the file as a case, and send it to wwxhero@163.com, so that I can analyze it later.
Points of Interest
The calculation error can overturn the logic, the theoretical stance of this algorithm was neglect to CPU calculation error, and this issue is critical especially with data type “int”, and for the cases the algorithm failed to triangulate the polygon are mostly caused by calculation error, therefore the implementation of the algorithm should use the logic calculation to replace arithmetic calculation if possible. While for the cases that the algorithm fails, please save the testing data to a file and send it to wwxhero@163.com.<o:p>
The algorithm will have poorer performance if there are dense points in a small region than the rasterization algorithm.
History
- 24th Jan, 2016: Bug fix: For the multiple overlapping edges intersecting in a single vertices geometrically, the winding number is not correctly calculated.
- 24th Jan, 2016: Port latest update to linux
- 17th Jan, 2016: Code complete for winding mode triangulation
- 10th Jan, 2016: Do not offset vertices during re-routing in order to avoid calculation based on error values
- 6th Jan, 2016: Bug fix: intersection test in even-odd mode
- 14th June, 2015: Initial version
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










