Introduction
Triangles are classified depending on relative sizes of their elements.
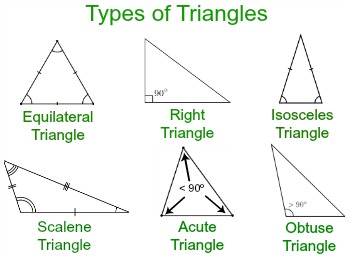
As regards their sides, triangles may be:
- Scalene (all sides are different)
- Isosceles (two sides are equal)
- Equilateral (all three sides are equal)
And as regards their angles, triangles may be:
- Acute (all angles are acute)
- Right (one angle is right)
- Obtuse (one angle is obtuse)
Obs:
- One of the properties of the triangles is that the sum of the lengths of any two sides is greater than the length of the third side.
- There is a special type of triangle, called a degenerate triangle. formed by three collinear points. It doesn’t look like a triangle, it looks like a line segment. In this case, one of its sides is equal to the sum of the other
In this tip, we will develop an algorithm that determines the type of a triangle, given its sides.
Using the Code
The algorithm below was implemented in the Lua language using the ZeroBrane Studio IDE:
--[[--
TriangleType
Determines the type of the triangle by the sides and by the angles
Language: Lua
2018, Jose Cintra
josecintra@josecintra.com
--]]--
-- Compare two floats
local function almostEquals(a, b)
threshold = 0.00001
diff = math.abs(a - b) -- Absolute value of difference
return (diff < threshold)
end
-- Determines the type of the triangle by the sides and by the angles
local function triangleType(a,b,c)
local bySide,byAngle = nil
if (a <= (b + c) and b <= (a + c) and c <= (a + b)) then
--Type of the triangle by sides
if ( a == b and b == c ) then
bySide = 1 -- Equilateral
elseif (a == b or b == c or a == c) then
bySide = 2 -- Isosceles
else
bySide = 3 -- Scalene
end
--Type of the triangle by Angle
if almostEquals(a,(b + c)) or almostEquals(b,(a + c)) or almostEquals(c,(a + b)) then
byAngle = 4 -- Degenerate
elseif almostEquals(a^2,(b^2 + c^2)) or almostEquals(b^2,(a^2 + c^2)) or almostEquals(c^2,(a^2 + b^2)) then
byAngle = 1 -- Right
elseif (a^2 > b^2 + c^2) or (b^2 > a^2 + c^2) or (c^2 > a^2 + b^2) then
byAngle = 2 -- Obtuse
else
byAngle = 3 -- Acute
end
end
return bySide,byAngle
end
-- Main routine
local bySideTypes = {"Equilateral","Isosceles","Scalene"}
local byAngleTypes = {"Right","Obtuse","Acute","Degenerate"}
print("Triangle Type\n")
print("Enter the value of A side: ")
local a = tonumber(io.read())
print("Enter the value of B side: ")
local b = tonumber(io.read())
print("Enter the value of C side: ")
local c = tonumber(io.read())
local bySide,byAngle = triangleType(a,b,c)
if (bySide ~= nil) then
print ("The type of the triangle is " .. bySideTypes[bySide] .. "/" .. byAngleTypes[byAngle])
else
print ("These sides do not form a triangle")
end
-- end
Points of Interest
The following points should be taken into account for the understanding of the algorithm:
- To obtain the type of the triangle according to its angles, we use the Pythagorean theorem. Like this.
- In the Lua language, a function can return more than one value.
- For comparison of float values, we use the
almostEquals function, which can be adjusted according to your need, in the threshold variable. - For the sake of "good practices", we have resolved to encode the types of triangles in an array.
History
21 Oct 2018 - Initial version
27 Oct 2018 - Added "degenerate triangles" and almostEquals function
References
- https://study.com/academy/lesson/types-of-triangles-their-properties.html
- https://www.youtube.com/watch?v=I2Lt-jU3IJc
Last Words
Thanks for reading!
The source code for this algorithm is also available on GitHub at: MathAlgorithms
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 








