Text Documents Clustering using K-Means Algorithm

• Download source code - 53.5 KB 

Introduction

Clustering can be considered the most important unsupervised learning problem; so, as every other problem of this kind, it deals with finding a structure in a collection of unlabeled data. A loose definition of clustering could be “the process of organizing objects into groups whose members are similar in some way”. A cluster is therefore a collection of objects which are coherent internally, but clearly dissimilar to the objects belonging to other clusters.

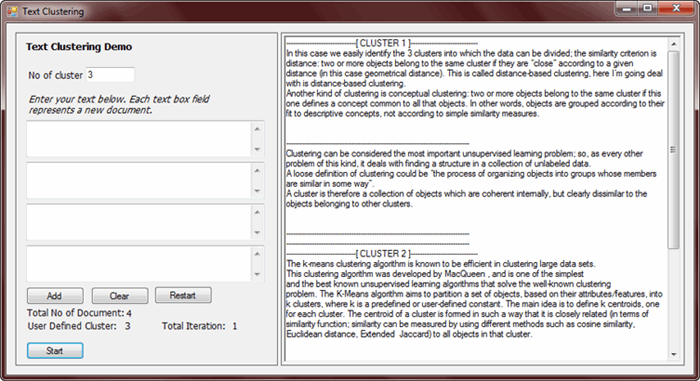
In this case we easily identify the 3 clusters into which the data can be divided; the similarity criterion is distance: two or more objects belong to the same cluster if they are “close” according to a given distance (in this case geometrical distance). This is called distance-based clustering, here I’m going to deal with is distance-based clustering. Another kind of clustering is conceptual clustering: two or more objects belong to the same cluster if this one defines a concept common to all that objects. In other words, objects are grouped according to their fit to descriptive concepts, not according to simple similarity measures.

Classification

Clustering algorithms may be classified as listed below

1. Flat clustering (Creates a set of clusters without any explicit structure that would relate clusters to each other; It’s also called exclusive clustering)
2. Hierarchical clustering (Creates a hierarchy of clusters)
3. Hard clustering (Assigns each document/object as a member of exactly one cluster)
4. Soft clustering (Distribute the document/object over all clusters)

Algorithms

1. Agglomerative (Hierarchical clustering)
2. K-Means (Flat clustering, Hard clustering)
3. EM Algorithm (Flat clustering, Soft clustering)

Hierarchical Agglomerative Clustering (HAC) and K-Means algorithm have been applied to text clustering in a straightforward way. Typically it usages normalized, TF-IDF-weighted vectors and cosine similarity. Here, I have illustrated the k-means algorithm using a set of points in n-dimensional vector space for text clustering.

K-Means Algorithm

The k-means clustering algorithm is known to be efficient in clustering large data sets. This clustering algorithm was developed by MacQueen , and is one of the simplest and the best known unsupervised learning algorithms that solve the well-known clustering problem. The K-Means algorithm aims to partition a set of objects, based on their attributes/features, into k clusters, where k is a predefined or user-defined constant. The main idea is to define k centroids, one for each cluster. The centroid of a cluster is formed in such a way that it is closely related (in terms of similarity function; similarity can be measured by using different methods such as cosine similarity, Euclidean distance, Extended Jaccard) to all objects in that cluster.

Basic K-Means Algorithm

1. Choose k number of clusters to be determined
2. Choose k objects randomly as the initial cluster center
3. Repeat  

3.1. Assign each object to their closest cluster
3.2. Compute new clusters, i.e. Calculate mean points. 
    4. Until 
        4.1. No changes on cluster centers (i.e. Centroids do not change location any more) OR
        4.2. No object changes its cluster (We may define stopping criteria as well) 

Residual Sum of Squares

RSS is a measure of how well the centroids represent the members of their clusters, the squared distance of each vector from its centroid summed over all vectors.

The algorithm then moves the cluster centers around in space in order to minimize RSS

Termination Condition

We can apply one of the following termination conditions.

• A fixed number of iterations I has been completed. This condition limits the runtime of the clustering algorithm, but in some cases the quality of the clustering will be poor because of an insufficient number of iterations.
• Assignment of documents to clusters does not change between iterations. Except for cases with a bad local minimum, this produces a good clustering, but runtimes may be unacceptably long.
• Centroids do not change between iterations. This is equivalent to not Terminate when RSS falls below a threshold. This criterion ensures that the clustering is of a desired quality after termination. In practice, we need to combine it with a bound on the number of iterations to guarantee termination.
• Terminate when the decrease in RSS falls below a threshold t . For small t, this indicates that we are close to convergence. Again, we need to combine it with a bound on the number of iterations to prevent very long runtimes.

Bad choice of initial seed

In K-Means algorithm there is unfortunately no guarantee that a global minimum in the objective function will be reached, this is a particular problem if a document set contains many outliers , documents that are far from any other documents and therefore do not fit well into any cluster. Frequently, if an outlier is chosen as an initial seed, then no other vector is assigned to it during subsequent iterations. Thus, we end up with a singleton cluster (a cluster with only one document) even though there is probably a clustering with lower RSS.

Effective heuristics for seed selection include:

1. Excluding outliers from the seed set
2. Trying out multiple starting points and choosing the clustering with the lowest cost; and
3. Obtaining seeds from another method such as hierarchical clustering.

Diving into the code

Document Representation

Each document is represented as a vector using the vector space model. The vector space model also called term vector model is an algebraic model for representing text document (or any object, in general) as vectors of identifiers. For example, TF-IDF weight.

Here I have defined DocumentVector class whose instance holds the document and its corresponding representation on vector space.

public class DocumentVector
{
    //Content represents the document(or any other object) to be clustered
    public string Content { get; set; }
    //represents the tf*idf of  each document
    public float[] VectorSpace { get; set; }
}

And instance of DocumentCollection represtnts all the documents to be clustered

class DocumentCollection
{
    public  List<String> DocumentList { get; set; }
}

TF-IDF

TF-IDF stands for term frequency-inverse document frequency, is a numerical statistics which reflects how important a word is to a document in a collection or corpus, it is the most common weighting method used to describe documents in the Vector Space Model, particularly on IR problems.

The number of times a term occurs in a document is called its term frequency. We can calculate the term frequency for a word as the ratio of number of times the word occurs in the document to the total number of words in the document.

The inverse document frequency is a measure of whether the term is common or rare across all documents. It is obtained by dividing the total number of documents by the number of documents containing the term, and then taking the logarithm of that quotient.

The tf*idf of term t in document d is calculated as:

//Calculates TF-IDF weight for each term t in document d
private static float FindTFIDF(string document, string term)
{
   float tf = FindTermFrequency(document, term);
   float idf = FindInverseDocumentFrequency(term);
   return tf * idf;
}
 
private static float FindTermFrequency(string document, string term)
{
   int count = r.Split(document).Where(s => s.ToUpper() == term.ToUpper()).Count();
   //ratio of no of occurance of term t in document d to the total no of terms in the document
   return (float)((float)count / (float)(r.Split(document).Count()));
}
 
private static float FindInverseDocumentFrequency(string term)
{
   //find the  no. of document that contains the term in whole document collection
   int count = documentCollection.ToArray().Where(s => r.Split(
       s.ToUpper()).ToArray().Contains(term.ToUpper())).Count();
   /*
    * log of the ratio of  total no of document in the collection to the no. of document containing the term
    * we can also use Math.Log(count/(1+documentCollection.Count)) to deal with divide by zero case; 
    */
    return (float)Math.Log((float)documentCollection.Count() / (float)count);
}

Finding Similarity Score

I have used cosine similarity to identify the similarity score of a document. The method FindCosineSimilarity takes two argument vecA and vecB as parameter which are vector representation of document A and B, and returns the similarity score which lies between 1 and 0, indicating that document A and B are completely similar and dissimilar respectively.

public static float FindCosineSimilarity(float[] vecA, float[] vecB)
{
      var dotProduct = DotProduct(vecA, vecB);
      var magnitudeOfA = Magnitude(vecA);
      var magnitudeOfB = Magnitude(vecB);
      float result = dotProduct / (magnitudeOfA * magnitudeOfB);
      //when 0 is divided by 0 it shows result NaN so return 0 in such case.
      if (float.IsNaN(result))
          return 0;
       else
          return (float)result;
 }

K-Means Algorithm Implementation

To implement K-Means algorithm I have defined a class Centroid in which documents are assigned during the clustering process.

public class Centroid
{
    public List<DocumentVector> GroupedDocument { get; set; }
}

Preparing Document Cluster

public static List<Centroid> PrepareDocumentCluster(int k, 
          List<DocumentVector> documentCollection,ref int _counter)
{
   globalCounter = 0;
   //prepares k initial centroid and assign one object randomly to each centroid
   List<Centroid> centroidCollection = new List<Centroid>();
   Centroid c;
        
   /*
    * Avoid repeation of random number, if same no is generated 
    * more than once same document is added to the next cluster 
    * so avoid it using HasSet collection
    */
    HashSet<int> uniqRand = new HashSet<int>();
    GenerateRandomNumber(ref uniqRand,k,documentCollection.Count);
        
    foreach(int pos in uniqRand) 
    {
        c = new Centroid();                
        c.GroupedDocument = new List<DocumentVector>();
        c.GroupedDocument.Add(documentCollection[pos]);
        centroidCollection.Add(c);                
    }

    Boolean stoppingCriteria;
    List<Centroid> resultSet;
    List<Centroid> prevClusterCenter;
        
    InitializeClusterCentroid(out resultSet, centroidCollection.Count);

    do
    {
         prevClusterCenter = centroidCollection;

         foreach (DocumentVector obj in documentCollection)
         {
             int index = FindClosestClusterCenter(centroidCollection, obj);
             resultSet[index].GroupedDocument.Add(obj);
         }
         InitializeClusterCentroid(out centroidCollection, centroidCollection.Count());
         centroidCollection = CalculateMeanPoints(resultSet);
         stoppingCriteria = CheckStoppingCriteria(prevClusterCenter, centroidCollection);
         if (!stoppingCriteria)
         {   
             //initialize the result set for next iteration
              InitializeClusterCentroid(out resultSet, centroidCollection.Count);
         }

    } while (stoppingCriteria == false);

    _counter = counter;
    return resultSet;

}

Initializing cluster center

Cluster center is initialized for the next iteration, here the count variable holds the value of user defined initial cluster center.

private static void InitializeClusterCentroid(out List<Centroid> centroid,int count)
{
  Centroid c;
  centroid = new List<Centroid>();
  for (int i = 0; i < count; i++)
  {
       c = new Centroid();
       c.GroupedDocument = new List<DocumentVector>();
       centroid.Add(c);
  }
} 

Finding closest cluster center

This function returns the index of closest cluster center for each document, I have used cosine similarity to identify the closeness of document. The array similarityMeasure holds the similarity score for the document obj with each cluster center, the index which has maximum score is taken as the closest cluster center of the given document.

private static int FindClosestClusterCenter(List<Centroid> clusterCenter,DocumentVector obj)
{
  float[] similarityMeasure = new float[clusterCenter.Count()];

  for (int i = 0; i < clusterCenter.Count(); i++)
  {
       similarityMeasure[i] = 
         SimilarityMatrics.FindCosineSimilarity(
         clusterCenter[i].GroupedDocument[0].VectorSpace, obj.VectorSpace); 
  }

  int index = 0;
  float maxValue = similarityMeasure[0];
  for (int i = 0; i < similarityMeasure.Count(); i++)
  {
       //if document is similar assign the document
       //to the lowest index cluster center to avoid the long loop
       if (similarityMeasure[i] >maxValue)
       {
           maxValue = similarityMeasure[i];
           index = i;
       }
   }
   return index;
}

Identifying the new position of the cluster center

After each document being assigned to its closest cluster center we recalculate the mean of each cluster center which indicates the new position of cluster center (centroid).

private static List<Centroid> CalculateMeanPoints(List<Centroid> _clusterCenter)
{
 for (int i = 0; i < _clusterCenter.Count(); i++)
 {
      if (_clusterCenter[i].GroupedDocument.Count() > 0)
      {
         for (int j = 0; j < _clusterCenter[i].GroupedDocument[0].VectorSpace.Count(); j++)
         {
              float total = 0;
                    
              foreach (DocumentVector vSpace in _clusterCenter[i].GroupedDocument)
              {
                   total += vSpace.VectorSpace[j];
              }
              //reassign new calculated mean on each cluster center,
              //It indicates the reposition of centroid
              _clusterCenter[i].GroupedDocument[0].VectorSpace[j] = 
                                  total / _clusterCenter[i].GroupedDocument.Count();
          }
      }
  }
  return _clusterCenter;
}