Introduction
Genetic Algorithms are part of Artificial Intelligence (AI). Actually, the concept of genetic algorithm is a copy from evolution in nature. New generations with more consistency and compatibility can surpass older generations, and they exchange their characteristics with the closest generations. This article shows how genetic algorithms can help us to classify our data based on a function called the genetic algorithm function.
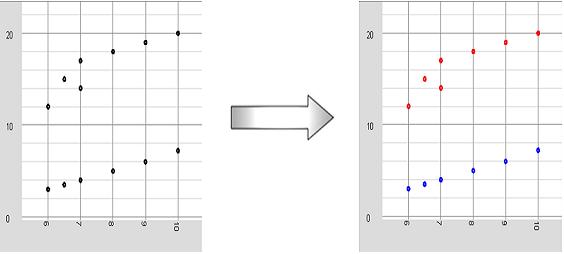
Imagine that we have data which is a combination of different data groups from zones with identical behavior. This means that, although each data group has its own functionality, the difference is only between function parameters. The graph below shows a number of points on the XY coordinate. Obviously our data is a combination of two data groups. Now lets imagine a condition at which we already know the formula and each group is generated by a y=ax+b function. In this example we do not face a serious problem in the classification while there are only two groups and data is separated clearly.
In more complex examples we cannot follow such procedures. For example, take the condition at which we have five different data groups in 1000 data sets which are dispersed in XY coordinates or at the intersection area of two or more data groups. Here human observation is not reliable enough for data classification. If we try to find the mean squared error (MSE) for different groups of data and functions we just waste the time, because in most of the case, billions of mathematical terms should be calculated. This is where we need genetic algorithm in such problem.

Background
This article does not cover all genetic algorithm subjects, but is simply an applied example of how to classify different data based on an available correlation. Let’s consider an array of data group indices. This array has a length equal to data sets count and for each data set (X and Y) it has its own group index inside its elements. For example, in the graph above we may have an array of 0 and 1 because this is supposed that we have only two data groups.

Such an array can occur in different forms, each of which has its own MSE based on the calculated parameters of our genetic algorithm functions (here y=ax+b). The figure below shows ten different forms of such an array. At the beginning we randomly set the values. Now our genetic algorithm begins.

First of all, the algorithm should calculate the MSE for all ten cases above. We call these cases genetic algorithm strings. Obviously each string has its own MSE. After calculating the error now we can guess the closer strings to our final classification. Here we sort the strings from best MSE to the worst. As a matter of fact, each guessed index has another MSE — by itself — inside the string. The evolution of the genetic algorithm depends on the better selection of elements to exchange. In other words, in order to choose the best element (to exchange) we have to know its MSE. For the highest values of such MSE we can say that the current element is not properly set so its value can be exchanged by the value in each element with similar characteristics at the nearby string.

So in the next step we start exchanging the high internal MSE elements of strings in such a way that each string exchanges values with the string at its neighborhood. This was the reason that our string count is even. The number of elements to exchange can be randomly set but for more reliable results and more stable algorithms it is better to have a smaller number of exchanges at each loop. In the figure above we have two exchanges in the first two strings, for other string pairs this number can be different. Here our first loop is accomplished. Now we have to re-start the procedure by re-calculating MSEs. So, the procedure in one loop consists of three steps:
- Calculating MSEs of strings and their elements
- Sorting strings based on MSEs
- Exchanging high error element values
Remember that this algorithm is one out of tens of algorithms can be utilized. We have many more methods and tricks for faster convergence but this example is simple and clear enough to understand and apply.
Using the Code
First of all we have to declare suitable data structures for our data treatments.
Structure of our Input Data
Structure DataGroup
Dim X() As Double
Dim Y() As Double
End Structure
Structure of Genetic Strings
Structure DataGroup
Dim X() As Double
Dim Y() As Double
End Structure
Structure of Regression Parameters
In order to evaluate MSE we have to fit our points to the GA function. The primary result of this fitting process is the regression parameter. In this case we supposed that the function is y=ax+b so the parameters are a and b.
Structure RegressionParameter
Dim a As Double
Dim b As Double
End Structure
Structure of Output
Obviously we need to check the responses from GA at each loop.
Structure OutPut
Dim RP() As RegressionParameter
Dim BestString As GeneticString
Dim MSE As Double
End Structure
Now the properties can be declared:
| Property | Type | Description |
Epoch | Integer | The maximum number of epochs |
MSE | Double | Desired MSE |
StringCount | Short | Number of strings in the algorithm |
GeneticString() | _GeneticString | Array of GA strings |
DataGroup | _DataGroup | Input data |
Output | _OutPut | Results from GA |
Two events are also declared: Epochs and Goalmet. Their names are straight-forward. The Epochs event will be executed whenever a loop is completed and Goalmet will be called when the maximum epoch is reached or the error goes under the desired MSE.
Based on three steps mentioned we can divide our subroutines and functions in three groups.
Calculating MSEs of Strings and their Elements
Sub CalculateBitError(ByRef GString As _GeneticString,
ByVal RParameter() As _RegressionParameter)
Function ReturnMSE(ByVal DGroup() As _DataGroup, ByVal RP() As _RegressionParameter)
Function FindPointMSE(ByVal X As Double, ByVal Y As Double,
ByVal RP As _RegressionParameter) As Double
Function FindMSE(ByVal X() As Double, ByVal Y() As Double,
ByVal RP As _RegressionParameter) As Double
Function PerformRegression(ByVal DGroup() As _DataGroup,
ByRef RP() As _RegressionParameter) As Boolean
Function LinearRegression(ByVal X() As Double, ByVal Y() As Double,
ByRef b As Double, ByRef a As Double) As Boolean
Sorting Strings Based on MSEs
Sub Sort(ByRef GString() As _GeneticString)
Sub Switch(ByRef Val1 As Double, ByRef Val2 As Double)
Exchanging High Error Elements Values
Sub BitExchange(ByRef STC() As _GeneticString)
Sub Exchange(ByRef STC1 As _GeneticString, ByRef STC2 As _GeneticString,
ByVal num As Integer)
Function PrepareDataGroup(ByVal LineCount As Integer, ByRef GString As _GeneticString,
ByVal X() As Double, ByVal Y() As Double) As _DataGroup()
The role of most of the above subroutines and functions is clear. All these codes are in the GA class so we have to instantiate this class.

Clicking the Classify button executes the code below. Here the GetXY subroutine returns the X and Y values in DataGridView.
Dim DG As New GA._DataGroup
GetXY(DG.X, DG.Y)
With GA
.DataGroup = DG
.StringCount = nud1.Value
.Epoch = TextBox1.Text
.MaxMSE = TextBox2.Text
.Run()
End With
The result will be saved in the Output property of GA and can be read from the GoalMet event handler. The best GA string — which is an array of 0 and 1 — can be used to represent our classification with different colors such as below. That’s all!

Copyright
The source code is entirely free. A control called IMP is used for plotting. This control is under construction and has bugs. I do not recommend you to use IMP in your projects.
Points of Interest
For more complex data sets such as intersection (as show below) it is better to have a higher epoch number. A higher string count can help us to have a stable algorithm but both reduce the convergence speed.


The code is written in VB.NET and is only a guide to write a genetic algorithm in such a case of study. In the case that the code is written in a .NET language it is not suitable for heavy mathematical tasks. This is better to re-write the code in a low-class language with a faster compiler.
I'm a Full-stack Software Developer with over a decade of experience at industrial and research projects having my main focus on Microsoft .Net stack.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







