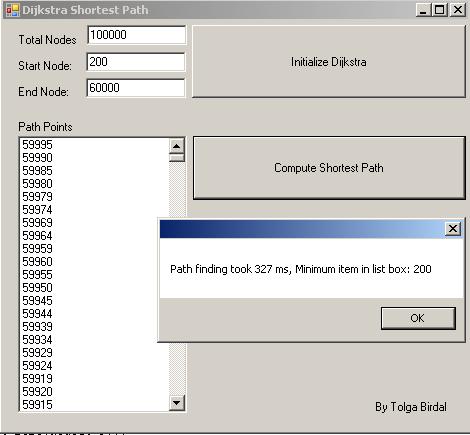
Introduction
Because I mainly work on image processing and computer vision, I post articles on solutions of what might be problems in signal processing, problem solving etc. Image segmentation tasks, most of the time, require a huge amount of computation. In such cases, the image is generally interpreted as a graph of pixels or graphs. One problem might be the shortest path in a given undirected, weighted graph.
At the beginning, my intention wasn't implementing this. Then, I realized that no one has put an implementation of an efficient Dijkstra algorithm for C#, that is suitable for my needs. Especially for a directed, weighted graph, it is hard to find a solution.
Background
To understand this article and to use the code appropriately, one needs to know what Dijkstra's algorithm does and what a heap (priority queue) is. Let's begin with Dijkstra's Algorithm.
Dijkstra's Algorithm:
For a given source vertex (node) in the graph, the algorithm finds the path with the lowest cost (i.e., the shortest path) between that vertex and every other vertex. It can also be used for finding costs of shortest paths from a single vertex to a single destination vertex, by stopping the algorithm once the shortest path to the destination vertex has been determined. For example, if the vertices of the graph represent cities and edge path costs represent driving distances between pairs of cities connected by a direct road, Dijkstra's algorithm can be used to find the shortest route between one city and all other cities.
The algorithm was invented by Edsger Dijkstra in 1959, and it is still one of the best solutions to the shortest path algorithm.
Here is a simple pseudo-code (it could vary from one implementation to another):
1 function Dijkstra(Graph, source):
2 for each vertex v in Graph: // Initializations
3 dist[v] := infinity // Unknown distance
// function from source to v
4 previous[v] := undefined
5 dist[source] := 0 // Distance from source to source
6 Q := copy(Graph) // All nodes in the graph
// are unoptimized - thus are in Q
7 while Q is not empty: // The main loop
8 u := extract_min(Q) // Remove and return best vertex
// from nodes in two given nodes
// we would use a path finding algorithm
// on the new graph,
// such as depth-first search.
9 for each neighbor v of u: // where v has not yet been removed from Q.
10 alt = dist[u] + length(u, v)
11 if alt < dist[v] // Relax (u,v)
12 dist[v] := alt
13 previous[v] := u
14 return previous[]
As seen, the previous[] array contains the path from one point to another. The bottleneck here is the extract_min function. Given an array, this function returns the minimum value. Naive implementations of the Dijkstra's Algorithm (mostly found on the web) use a linear array search to compute this minimum value. However, this approach yields very bad performance. Here is where the priority queue comes into play.
Priority Queue:
Priority Queues (Heaps) are very neat data structures allowing to:
- add an element to the queue with an associated priority
- remove an element from the queue that has the highest priority, and return it
- (optionally) peek at the element with the highest priority without removing it
A simple way to implement a priority queue data type is to keep a list of elements, and search through the list for the highest priority element for each "minimum" or "peek" operation. This implementation takes an O(1) time to insert an element, and an O(n) time for "minimum" or "peek". There are many more efficient implementations available. The Emde Boas implementation is one of the fastest ones, which has an O(log(log(n)) complexity for every operation.
For my implementation, I used BenDi's code, which is rather straightforward. I also modified it to have lesser complexity and lesser overhead by reducing the generality and using a List structure instead of an ArrayList. The code can be found here.
Resulting Algorithm:
What I used is a simple modified version of the above pseudo-code. Here is an overview of the pseudo-code:
Take the origin vertex, set the weight of the shortest path to 0 and
push it onto the priority queue.
while the priority queue is not empty, pop an entry <v,w_v,p_v>where
v is the vertex, w_v and p_v are the augmented labels of v.
foreach edge e=(v,u) in G, where u has augmented labels w_u, p_u.
if wt(e) + w_v < w_u then
set p_u to v
set w_u to wt(e) + w_v
add <u,>to the priority queue.
Using the Code
The Dijkstra class is very customizable. The idea is to assume a virtual graph (hypothetically). A graph is composed of a set of nodes, and weights assigned to each node. It is very likely to represent weights as travelling distances and nodes as vertexes. So, we have two arrays, one 2D and one 1D. In such a scenario, one should be able to provide the costs for each node and a neighbor list (the list of nodes that are connected to a given node). One could either pre-compute these values or provide these values at runtime. Pre-computation will yield a faster runtime performance, whereas it will require more memory and bandwidth. To use the code:
public delegate float InternodeTraversalCost(int start, int finish);
This delegate is the pointer to a function that returns a cost value for given start and finish nodes. You have to provide this function. In my case, it is an image, so I compute it by filling a 2D array by costs of pixels and nodes connected to it.
public delegate IEnumerable<int> NearbyNodesHint(int startingNode);
This delegate is the function pointer to a function that returns a list of nodes, given an input node. The list of nodes are simply the neighbors of (the nodes that are connected to) the given node. At the end, this is how we create the instance:
dijkstra = new DijkstraFast(totalNodes,
new DijkstraFast.InternodeTraversalCost(getInternodeTraversalCost),
new DijkstraFast.NearbyNodesHint(GetNearbyNodes));
The resulting code looks like this:
public virtual Results Perform(int start)
{
float[] d = GetStartingTraversalCost(start);
int[] p = GetStartingBestPath(start);
BasicHeap Q = new BasicHeap();
for (int i = 0; i != TotalNodeCount; i++)
Q.Push(i, d[i]);
while (Q.Count != 0)
{
int v = Q.Pop();
foreach (int w in Hint(v))
{
if (w < 0 || w > Q.Count - 1) continue;
float cost = TraversalCost(v, w);
if (cost < float.MaxValue && d[v] + cost < d[w])
{
d[w] = d[v] + cost;
p[w] = v;
Q.Push(w, d[w]);
}
}
}
return new Results(p, d);
}
The above algorithm uses the basic custom heap I have created. If you want to be more generic, I am also putting an implementation using BenDi's code:
public virtual Results Perform2(int start)
{
float[] d = GetStartingTraversalCost(start);
int[] p = GetStartingBestPath(start);
BinaryPriorityQueue Q = new BinaryPriorityQueue();
for (int i = 0; i != TotalNodeCount; i++)
Q.Push(new QueueElement(i,d[i]));
while (Q.Count!=0)
{
int v = ((QueueElement)Q.Pop()).index;
foreach (int w in Hint(v))
{
if (w <0 || w > Q.Count-1) continue;
float cost = TraversalCost(v, w);
if (cost < float.MaxValue && d[v] + cost < d[w])
{
d[w] = d[v] + cost;
p[w] = v;
Q.Push(new QueueElement(w, d[w]));
}
}
}
return new Results(p, d);
}
Points of Interest and Conclusion
The algorithm is easy to use and easy to upgrade. I will be looking for further implementations, using better heaps.
Have a nice coding...
History
Begins here...
